Another way to approach the xkcd-ification of plots is from an image processing perspective. The idea is to warp the space in which the image lies rather than to try and warp the lines themselves. When the image-space warps, the lines appear to vary in thickness.
First define the following function, which is nearly just a line with slope one. The important part is that it has small sinusoidal oscillations about this slope. A function that does this is
f[x_, freq_, str_] := 0.99 x + Sin[(freq + 12 Sin[4 Pi x]) x]/str ;
which has two parameters: one controls the frequency of the oscillation and the other controls the strength/amount of the warping. To see how this function can be applied to the image space, start with a simple plot (from Mr. Wizard's "the race"). Since the lines are so thin, they need to be widened, which is done here using erosion. The function f is applied to both the x and y directions (the pure functions #[[1]] and #[[2]]) using ImageTransformation
plot = Plot[{x/2, (x + Sin[x])/2.2}, {x, 0, 2 Pi},
Frame -> {True, True, False, False}, FrameTicks -> None]
ImageTransformation[Erosion[Image[plot], 1],
{f[#[[1]], 80, 500], f[#[[2]], 105, 500]} &]

If there are no thin lines, there is no need to do the erosion:
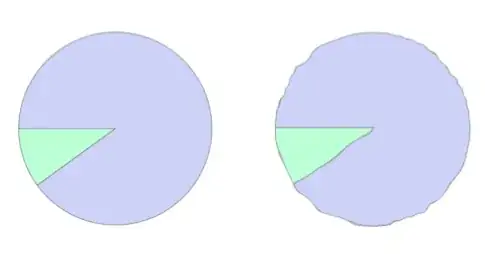
GraphicsRow[{piePlot = Image[PieChart[{9, 1}]],
ImageTransformation[piePlot, {f[#[[1]], 70, 180], f[#[[2]], 80, 180]} &]},
ImageSize -> 500]
Here's another example (taken from Mr. Wizard's answer) of this image transformation
GraphicsRow[{plot3 =Plot[{3 Sin@x, Cos@x, Tan[x]}, {x, 0, 2 Pi},
MaxRecursion -> 0, PlotPoints -> 30, PlotRange -> {-2, 2},
Frame -> {True, True, False, False}, FrameTicks -> None, Axes -> False],
ImageTransformation[ Erosion[Image[plot3], 1],
{f[#[[1]], 64, 300], f[#[[2]], 80, 400]} &]}, ImageSize -> 600]

Using a Manipulate, it is easy to explore a fairly wide variety of hand-drawn effects. Using the plot from above
Manipulate[
ImageTransformation[ Erosion[Image[plot],1],
{f[#[[1]], freq, m], g[#[[2]], freq + 10, m]} &],
{{freq, 40,"frequency"}, 0, 200}, {{m, 500, "strength"}, 100, 1000, 10}]

The same idea an also be applied to text
text = Style["Every font is comic sans", FontSize -> 50, FontFamily -> "Geneva"]
ImageTransformation[Image[Rasterize[text]],
{f[#[[1]], 64, 200], f[#[[2]], 90, 200]} &]

which has the interesting property that different occurrence of a letter will not be the same (because they are warped differently by the underlying space). In this example, notice how the three s's, two n's and c's differ from each other.
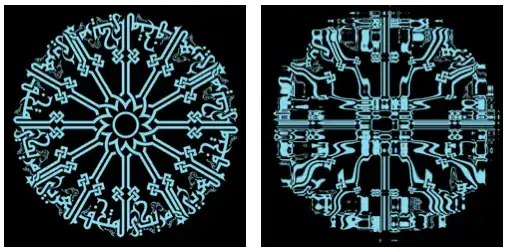
And finally (I promise to stop adding new examples) it can be applied to any image. Here is a pattern that shows how the underlying space is warped by the function f:
GraphicsRow[{img2 = ColorNegate[Import["https://i.stack.imgur.com/F8Plt.png"]],
ImageTransformation[img2,{f[#[[1]], 90, 100], f[#[[2]], 80, 50]} &]},
ImageSize->500]
And here is a full StackExchange xkcdified plot using the above transformation. The bulk of the code handles the labels and coloring. The Tooltip allows a secret mouse-over message, in the best xkcd tradition.
f[x_, freq_, str_] := 0.99 x + Sin[(freq + 12 Sin[4 Pi x]) x]/str;
fTicks = {{{{0.2, "hmm"}, {0.8, "wow!"}}, {{0.2, "boring"}, {0.8, "very\nboring"}}}, {{{0.2, "not enough"}, {0.8, "too much"}}, None}};
fLabels = {{Style["Today's StackExchange\nquestions", FontSize -> 13, Darker[Red]], Rotate[Style["Today's work", FontSize -> 13, Darker[Blue]], Pi]}, {Style["Time spent on Mathematica StackExchange", FontSize -> 13, Black], None}};
tip = Style["This seems to be a complex optimization problem.\nCan someone write the code for me?", FontFamily -> "Comic Sans MS", FontSize -> 13];
fTickStyle = {{Darker[Red], Darker[Blue]}, {Black, None}};
plot1 = Plot[{x^2, Exp[- 2 x]}, {x, 0, 1}, Axes -> False];
plot2 = Plot[None, {x, 0, 1}, PlotRange -> {0, 1}, Frame -> {{True, True}, {True, None}}, FrameTicks -> fTicks, FrameTicksStyle -> fTickStyle, LabelStyle -> Directive[FontFamily -> "Comic Sans MS"], FrameLabel -> fLabels];
xkcdified = ImageTransformation[ Erosion[Image[plot1], 2], {f[#[[1]], 80, 500], f[#[[2]], 105, 500]} &];
Tooltip[ImageCompose[ImageResize[Image[plot2], 600], ImageResize[xkcdified, 350],{Center, 210}], tip]



























Textin combination withGraphicsinstead ofPlotLegend. – VLC Oct 01 '12 at 07:47pts = Table[{x, 5*Sin[x]/x}, {x, 0.01, 10, 0.1}]; pts2 = pts + RandomReal[{-0.1, 0.1}/2, Dimensions[pts]]; f = BSplineFunction[pts2]; ParametricPlot[f[x], {x, 0.1, 0.9}, PlotStyle -> {Darker[Cyan, 0.3], AbsoluteThickness[3]}]– chris Oct 01 '12 at 09:09