Coloring specific set of points in a plot

Question

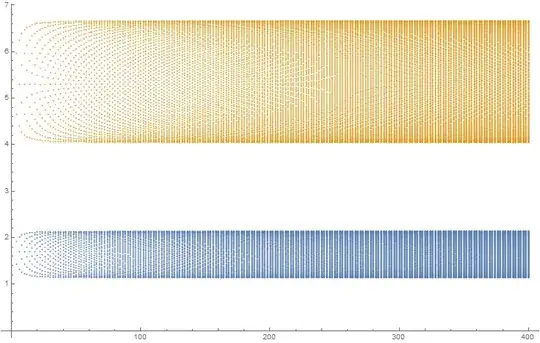
I have a large set of points.I get two bands of points in the graph which merge upon choosing suitable value of the parameters E1 and E2. My question is how to color these two sets of points differently to show how they are merging. . . 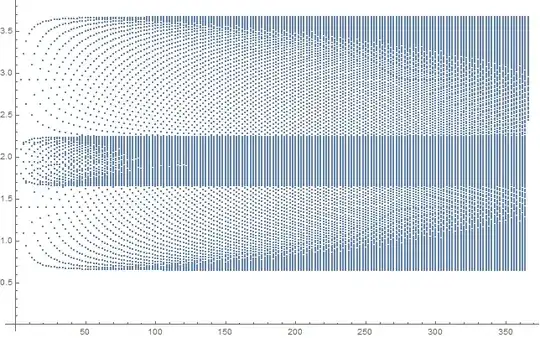The code for the second graph is as follows:

Data1 = {};
Data2 = {};
E1 = 2.1;
E2 = 2;
t = 0.1;
g11 = 0.5;
g21 = 0.3;
g22 = 0.4;

For[n = 4, n <= 100, n += 2,

M = SparseArray[{Band[{1, 1}, {n, n}] -> {E1, E2}, 
Band[{2, 1}, {n, n - 1}] -> {t, g21}, 
Band[{1, 2}, {n - 1, n}] -> {t, g21}, 
Band[{1, 3}, {n - 2, n}] -> {g11, g22}, 
Band[{3, 1}, {n, n - 2}] -> {g11, g22}, 
Band[{1, 4}, {n - 3, n}] -> {g21, 0}, 
Band[{4, 1}, {n, n - 3}] -> {g21, 0}}, {n, n}]; 


EigenList = {};
EigenVal = N[Eigenvalues[M], 3];



For[i = 1, i <= n, i++,
EigenList = {n, EigenVal[[i]]};
AppendTo[Data1, EigenList];
];
];

ListPlot[Data1]

The list Data1 takes in all the co-ordinates. There are degenerate states and so for same value of x we can get as many values of y.E.g.{1,a},{2,a1},{2,a2},{3,a3},{3,a4,{3,a5},{4,a6},{4,a7},{4,a8},{4,a9},{5,a10}.....

The question is not really about how to color them differently but rather how to identify the two groups. When they are distinct that is not too difficult. For this case the two groups are set by dividing each group of n by two. However, when they merge, this doesn't work. Perhaps you can add something about the algorithm that produces them. — Jack LaVigne, Jan 12 '17 at 19:08

score 3 · Accepted Answer · answered Jan 15 '17 at 04:33

By observing the data, it's not hard to notice the "dense" set of points belongs to the middle part of eigenvalue list, so:

E1 = 2.1;
E2 = 2.;
t = 0.1;
g11 = 0.5;
g21 = 0.3;
g22 = 0.4;
Data1 = {Flatten[#2, 1], Flatten[{#, #3}, 2]} & @@ 
   Transpose@Table[
     Internal`PartitionRagged[
      Thread@{n, 
        Eigenvalues@
         N@SparseArray[{Band[{1, 1}, {n, n}] -> {E1, E2}, 
            Band[{2, 1}, {n, n - 1}] -> {t, g21}, Band[{1, 2}, {n - 1, n}] -> {t, g21}, 
            Band[{1, 3}, {n - 2, n}] -> {g11, g22}, 
            Band[{3, 1}, {n, n - 2}] -> {g11, g22}, 
            Band[{1, 4}, {n - 3, n}] -> {g21, 0.}, 
            Band[{4, 1}, {n, n - 3}] -> {g21, 0.}}, {n, n}]}, 
       {Floor[n/4], n - 2 Floor[n/4], Floor[n/4]}], {n, 4, 100, 2}];

ListPlot[Data1]

Mathematica graphics

I would be grateful, if you could explain to me what you just did. It is great by the way. Thanks. — Mathematica Noob, Jan 16 '17 at 14:23
@MathematicaNoob I just made some list manipulations, read the document of those functions (by pressing F1) and you'll understand their usage. You may also want to read this and this post. As to Internal`PartitionRagged, check this post. — xzczd, Jan 16 '17 at 15:13

Coloring specific set of points in a plot

1 Answers1