I love the shorthand /@. It is amazing for readability (and laziness when typing). However, right now I find that I need Map at level 2, i.e. Map[f, List[List[a,b],List[c,d]], {2}], a lot and I'd wish there was a similar shorthand notation available for a map at level 2. Is there? If not, can we make one?
2 Answers
Corrected to use SubscriptBox as Rojo showed and Kvothe commented, fixing binding.
Rojo shows a way in Is it possible to define custom compound assignment operators like ⊕= similar to built-ins +=, *= etc?
MakeExpression[RowBox[{f_, SubscriptBox["/@", n_], expr_}], StandardForm] :=
MakeExpression @ RowBox[{"Map", "[", f, ",", expr, ",", "{", n, "}", "]"}]
Now, entered using Ctrl+-:
I actually used this (or code very like it) for a while but I got tired of having to translate to the long form for posting here so I stopped.
You could use a variation of you want to allow for full levelspec rather map at (only) level n.
Performance
Syntactically I like Kuba's suggestion of Map[f] /@ expr but I have personally rejected this as a general replacement for Map[f, expr, {2}], and I would like to illustrate why.
An aside: the only reason I am offering this critique is because I find this form desirable; I had the same reaction as march, just longer ago: "That's the usefulness of operator forms that I've been waiting for." I still hope that at least the performance aspect will be improved in future versions.
Unfortunately in the current implementation (or at least 10.1.0, but I don't think this has changed in v11) Operator Forms cannot themselves be compiled, therefore Map[f] /@ expr forces unpacking of expr. To make a contrived example where the Operator Form is at a stark disadvantage I shall use an array of many rows and few columns.
big = RandomReal[1, {500000, 3}];
Map[Sin] /@ big // RepeatedTiming // First
Map[Sin, big, {2}] // RepeatedTiming // First
1.160.0482
On["Packing"];
Map[Sin] /@ big;
Unpacking array with dimensions {500000,3} to level 1. >>
Unpacking array with dimensions {3}. >>
Unpacking array with dimensions {3}. >>
Unpacking array with dimensions {3}. >>
Further output of Developer`FromPackedArray::punpack1 will be suppressed during this calculation. >>
As LLlAMnYP commented one can see that the Operator Form is the problem here by comparing:
On["Packing"]
Sin /@ # & /@ big; // RepeatedTiming // First
0.0765
Here Sin /@ # & compiles and the operation is fast and no unpacking takes place.
Evaluation
At risk of belaboring a point there is another limitation or at least difference regarding Map[f] /@ expr: evaluation.
Compare:
Map[f, Hold[{a}, b, c], {2}]
Map[f] /@ Hold[{a}, b, c]
Hold[{f[a]}, b, c]Hold[Map[f][{a}], Map[f][b], Map[f][c]]
Clearly these operations are not equivalent.
-
1And its may be beside the point, but the
ListableSin[big]is yet a further order of magnitude faster. By the way, what aboutf /@ # & /@ exprin terms of unpacking? The operator form seems to unpack completely, while the stringed mapping operators unpack only one level? – LLlAMnYP Feb 02 '17 at 07:56 -
Great, thank you. One question: Do I understand correctly that your solution at the top of your post does not take a performance hit?
Also I don't know whether this might depend on the version or setup ,but my mathematica will try to complete my expression wrongly if I use the superscript (it will change the expression to (f /@)^2, so to avoid this inconvenience I changed the Superscript to a Subscript.
– Kvothe Feb 02 '17 at 09:57 -
@LLlAMnYP (1) Yes of course, re: #4 in (7925); I did warn that the example was contrived. (2) Yes
Sin /@ # & /@ bigis much better and I should have included that example as that was actually a key point: it is the Operator Form that interferes with this application. – Mr.Wizard Feb 02 '17 at 12:28 -
@Kvothe The overhead of this method manifests in a different place; see http://mathematica.stackexchange.com/a/39675/121 for one example of this. A single rule like this should have negligible overhead and I now prefer this method (as commented to Rojo) to using the Notation Package for this reason. (2) You're absolutely right and I mucked this up. For some reason I remembered it being Superscript despite Rojo's code, then I was surprised by the need to select
/@before entering the superscript to enforce binding (which I did mention by the way). I'll change this to Subscript. Thanks! – Mr.Wizard Feb 02 '17 at 12:32 -
@Mr.Wizard: Yes I see that you did mention that. Sorry, glancing over it I thought you were just explaining how to do superscripts (I thought: "wow he's really making it newbie ready") and I did not pay enough attention to it. – Kvothe Feb 02 '17 at 14:58
I'm not aware of a simple one, but perhaps you could make your own? The following is not great because it requires you to enter CenterDot as Esc+.+Esc, and you can't control the precedence, but depending on your use-case, it might be useful. In addition, you can use whatever built-in symbol with no built-in meaning you want:
CenterDot[f_, a_] := Map[f, a, {2}]
Then:
The CenterDot operator has no associativity which means that a string of input like a·b·c·d will be translated as CenterDot[a, b, c, d] which has no rule:
a·b·c·d // FullForm
CenterDot[a, b, c, d]
For this reason it is desirable to manually establish associativity:
CenterDot[a__, b_, c_] := a·(b·c)
Now:
a·Row[{b}]·Row[{c}]·Row[{d}]
a[b[c[d]]] (* Row[{a[Row[{b}][Row[{c}][d]]]}] *)
- 23,399
- 2
- 44
- 100
-
Thanks. Can I ask a few follow up questions. I've already used CenterDot (for an innerproduct where this symbol is conventional and thus very good for readability ). Are there good alternatives available , i.e. not to crazy a precedence, a short esc esc shorthand. (I did look in the documentation for Operators without Built‐in Meanings, but it does not give a complete list. (Which I find strange, is there something I don't understand about how the Mathematica documentation works?) – Kvothe Feb 02 '17 at 09:49
-
@Kvothe I don't know why that page is incomplete; I believe http://reference.wolfram.com/language/tutorial/OperatorInputForms.html is a better reference. Try
SmallCircle, shorthand entered EscscEsc. – Mr.Wizard Feb 02 '17 at 12:53 -
@Kvothe The
Precedencefunction may be useful as well; see http://mathematica.stackexchange.com/a/30430/121 for a few examples. Beware that its output is sometimes conflicting however. – Mr.Wizard Feb 02 '17 at 12:57 -
march I made an extension to your answer, hopefully correctly after a second attempt. I think it is an important point to address. – Mr.Wizard Feb 02 '17 at 13:31
-
@Mr.Wizard. Thanks for the extension. That makes good sense to do and isn't really something I would have thought of. – march Feb 02 '17 at 16:55
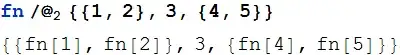

Map[f] /@ {{1, 2}}? you can always define new functionmap2[f,l]. – Kuba Feb 01 '17 at 18:45Mapand/@. – Kuba Feb 01 '17 at 21:01