How does Internal`CompareNumeric work?

Question

In this answer, Oleksandr R. mentioned an undocumented function Internal`CompareNumeric and briefly explained its usage as follows:

Internal`CompareNumeric[prec, a, b] returns -1, 0, or 1 according to whether a is less, equal, or greater than b when compared at the precision of a or b (whichever is less) minus prec decimal digits of "tolerance". It is the fundamental operation underlying Less, Equal, Greater, LessEqual etc. for finite-precision numeric types.

…To be honest, I failed to understand this description. In my eyes, it seems to suggest that, Internal`CompareNumeric will compare

With[{minPre = Precision /@ {a, b} // Min}, N[{a, b}, minPre - prec]]

but it's not true, because

Internal`CompareNumeric[1, 1.1`2, 1.2`2]
(* -1 *)

while the output should be 0 in my understanding.

Can someone explain the usage of Internal`CompareNumeric in a more detailed way?

Answer 1

This is just to highlight another aspect of the other answer given. I would have expected a linear progression from the definition. I.e., if Precision[n]=p then we'd expect the switch point for CompareNumeric[x, n, n+epsilon] to be p. And this holds once you get past $MachinePrecision. Probably happens when Mathematica has to go from 64 bit numbers to whatever its internal infinite-precision numeric is. We can see this here:

pr[x_] :=
  SelectFirst[
   Range[1, 100, .1],
   Internal`CompareNumeric[#, SetPrecision[1.1`, x], 1.2`100] == 0 &
   ];

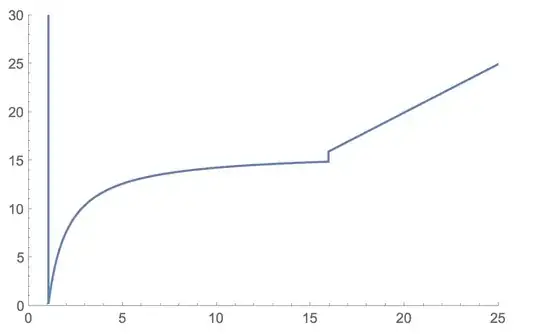
Show[
 Plot[x, {x, 0, 25}, PlotStyle -> Gray],
 {#, pr@#} & /@ Range[1, 25, .01] // ListPlot
 ]

I looked at the part for n < $MachinePrecision and thought: "oh, a log-type function (probably log2)". But no simple scaling on Log2 worked for me.

Show[ListLinePlot@Table[Table[x*N@Log2[n], {n, 15}], {x, 5}], 
 ListPlot[{#, pr@#} & /@ Range[1, 15, .01]]]

So maybe someone else can tackle what sort of pre-form that is. Once we have that we can probably piece back how Mathematica is interpreting things for its sub-machine precision numbers.

Update

As found by happy fish, $MachinePrecision - $MachinePrecision/x fits this really well:

Plot[{
  pr[x],
  $MachinePrecision - $MachinePrecision/x
  },
 {x, 1, $MachinePrecision}
 ]

Noting that $MachinePrecision is 53Log10[2] by simple log rearrangements we have Log10[2^(53*(1 - 1/x))]. Since $MachinePrecision comes from how a 64 bit number is stored (there are 53 bits of precision), this could be saying it's using 53*(1 - 1/x) bits of precision for these numbers with Precision specified below $MachinePrecision. Why that would be, I have no idea. But it's a possibility.

Update 2

Shadowray points out this is even odder when you have fewer points of precision available before they would be equivalent

For example, make pr multivariate:

pr[x_, y_: 1] :=
  SelectFirst[
   Range[1, 100, .1],
   With[{
     a = SetPrecision[1. + (10^(-y)), x],
     b = SetPrecision[1. + (2*10^(-y)), 100]
     },
    Internal`CompareNumeric[#, a, b] == 0 &
    ]
   ];

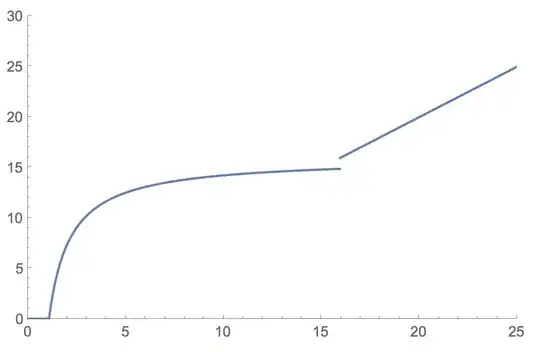
Now plotting this for different amounts of reduction:

Show[
 Plot[x, {x, 0, 25}, PlotStyle -> Gray],
 Table[
   {#, pr[#, n]} & /@ Range[1, 25, .05],
   {n, 17}
   ] // ListPlot
 ]

Note that the first 6 curves actually continue. They just jump up to y=x after $MachinePrecision (as I would naively have predicted).

If we use a near-continuous change:

Show[
 Plot[x, {x, 0, 25}, PlotStyle -> Gray],
 Table[
   {#, pr[#, n]} & /@ Range[1, 25, .05],
   {n, Range[1, 17, .1]}
   ] // ListPlot
 ]

The pre-discontinuity part can still be easily formulated:

Show[
 Plot[x, {x, 0, 25}, PlotStyle -> Gray],
 Plot[
  Evaluate@Table[$MachinePrecision (1 - n/x),
    {n, 16}],
  {x, 1, $MachinePrecision}],
 Table[
   {#, pr[#, n]} & /@ Range[1, 25, .1],
   {n, 17}
   ] // ListPlot
 ]

What's happening at the discontinuities is somewhat less clear. Note that the oddity at 17 is from the fact that 10^-17 is smaller than 10^-$MachinePrecision and so the system just treats the addition as doing nothing. The jumps need more explanation though.

In any case, if we return to the storage argument, now we have 53 n/x bits being dropped, assuming the interpreting the pre-jump part of the curves as showing Log10[2^(53 (1 - n/x))] is valid.

Answer 2

After some experiments I found some of the "rules" with which Internal`CompareNumeric[c, a, b] operates. If you find any exceptions please notify me. Lets denote minpr = Min[Precision[a],Precision[b]]. If c is greater than pr[minpr] then Internal`CompareNumeric[c, a, b] kind of throw away anything after the point. The function pr depends on a and b, the only symmetry I was able to detect is that if minpr>15, pr[minpr]=minpr (maybe connected to MachinePrecision?). The following figure is a possible pr[].

Answer 3

In this answer I will present an overall simulation of Internal`CompareNumeric's behavior. Throughout this answer, there are four variables: Internal`CompareNumeric[tol, a, b], first=Min[Abs[a],Abs[b]] diff=Abs[a-b] and prec is the minimum precision of the two specified. Here's my findings so far

• For exact arithmetic, Internal`CompareNumeric gives correct answer regardless of tol.
• For machine precision integers (1., 2.), the split point is always $MachinePrecision.
• The order and sign of a, b does not matter, the minimum precision is used for calculation(this can be implied from my definition above).
• The smallest prec that makes the two numbers comparable is $-\log_{10}(\frac{diff}{first+diff})$ (this number comes from the definition of Precision), i.e. when $prec>-\log_{10}(\frac{diff}{first+diff})$, there exist a tol, such that the function returns -1 or 1; when prec is less than this number, the function returns 0 for all tol settings.
• When $prec\in [-\log_{10}(\frac{diff}{first+diff}),\$MachinePrecision]$, there exist a split point $y$, such that when $tol<y$, the function returns -1 or 1, when $tol>y$, the function returns 0. The analytical formula with first, diff, prec as parameters is $$y(first,diff,prec)=\$MachinePrecision (1+\frac{1}{prec}\log_{10}(\frac{diff}{first+diff}))$$
• For prec>$MachinePrecision, the split point of tol is exactly the same as prec.
• For prec>$MachinePrecision, the formula above is incorrect. Some experiments show that when the ratio of first and diff is big enough, the comparison is converted to exact arithmetic(independent of tol). There should be two such points when diff/first is small and big, I haven't worked on it yet. A quick fixed of the formula is y[prec,first,diff]=prec-If[#>8,#,0]&[-Log10[diff/(first+diff)]], I will make careful research later when I have time.

The following is the code version of the findings above:

fishCompareNumeric[tol_, a_, b_] := 
 With[{first = Min[Abs@a, Abs@b], diff = Abs[a - b], prec = Precision@{a, b}},
  Module[{split},
   Catch[
    split = Piecewise[{
       {Throw@Sign[a - b], prec === Infinity},
       {$MachinePrecision, prec === MachinePrecision},
       {Throw@0, prec < -Quiet@Log10[diff/(first + diff)]},
       {$MachinePrecision (1 + Log10[diff/(first + diff)]/prec), -Log10[diff/(
           first + diff)] <= prec <= $MachinePrecision},
       {prec, prec > $MachinePrecision}
       }];
    Piecewise[{
      {Sign[a - b], tol < split}
      }]]]]

Here is a plot of my binary search for approximate values, with parameters(OP's example) first=1.1, diff=0.1, horizontal axis being prec and vertical axis being split point (of tol).

You may notice the two vertical lines at around 1.07 and 16, they are introduced by the sudden value changes, at the two points in my formula.

Here is a plot of my exact formula with same parameters

Code for binary search approximation:

splitPointBinary[{{val1_, val2_}, {low_, up_}}] := 
 With[{mid = Internal`CompareNumeric[(low + up)/2, val1, val2]}, 
  If[Internal`CompareNumeric[low, val1, val2] == 
    mid, {{val1, val2}, {(low + up)/2, up}}, {{val1, 
     val2}, {low, (low + up)/2}}]]
splitPointApprox[first_, diff_, prec_] := 
 FixedPoint[
   splitPointBinary, {{SetPrecision[first, prec], 
     SetPrecision[first + diff, prec]}, {0.1, 1000}}][[2, 1]]

Code for my formula:

splitPoint[first_, diff_, prec_] := 
 Piecewise[{{$MachinePrecision (1 + Log10[diff/(first + diff)]/prec), 
    -Log10[diff/(first + diff)] < prec < $MachinePrecision}, {prec, 
    prec > $MachinePrecision}}]

For OP's example,

splitPointApprox[1.1, 0.1, 2]
(*7.34564*)
splitPoint[1.1, 0.1, 2]
(*7.34564*)

Another one,

splitPointApprox[2.2, 0.5, 6]
(*14.0071*)
splitPoint[2.2, 0.5, 6]
(*14.0071*)

Answer 4

Let's consider a slightly different approach than above. For Internal`CompareNumeric[prec, a, a+ε], lets fix prec and a and find the threshold value for ε for which this switches from 0 to -1. For this purpose I define the following function

tf[p_?NumericQ, y_?NumericQ, z_?NumericQ] :=
   Internal`CompareNumeric[
     p,
     SetPrecision[1, y],
     SetPrecision[1, y] + 10^-SetPrecision[z, 100]
]

That is we take a = SetPrecision[1, y] and ε = 10^-SetPrecision[p, 100]. (The SetPrecision in the definition of ε is there to avoid that the precision of z in the input can affect the outcome in anyway.)

We can then find the threshold value using simple bisection. For example abusing FindRoot:

tf2[p_?NumericQ, y_?NumericQ] := (z /. 
  FindRoot[tf[p, y, z] == -1/2, {z, -10, p + y + 1}, 
  WorkingPrecision -> 100, MaxIterations -> 20])

Plotting the threshold value as a function of y for values of p we get

The top curve (p=0) is simply given by z = y. More generally the behavior of tf2 is modelled precisely by

Max[
 Piecewise[
  {
   {y - p, y > MP},
   {((MP - p)/MP) y, y < MP}
  }
 ],
 MP/2 UnitStep[y - Max[MP, p]]
]

where

MP=$MachinePrecision

What does this tell us about the behavior of Internal`CompareNumeric[prec,a,b]? Well, if the precision of a and b is set higher than machine precision and prec is not too large, the behavior is exactly as described by Oleksandr R.

It becomes a bit weirder when prec is large (compared to the precision of a and b), in which case there is an apparent upperbound of on the threshold difference of ε = 10^(-MP/2).

I don't quite understand the behavior of the threshold when the precision of a and b is smaller than machine precision. Maybe somebody else can shed some light.

Update:

Based on the above we can venture to propose a mock version of Internal`CompareNumeric[prec, a, b]:

MockCompareNumeric[p_,a_,b_]:=With[
 {ip = Min[Precision[a], Precision[b]]},
  With[
   {ep = Which[
    ip === MachinePrecision, MP-p
    ip >= Max[MP, p], Max[ip - p, MP/2],
    True, Max[(1 - p/MP) ip, 0]
    ]
   },
   If[N[ Abs[a - b]/Max[Abs[a], Abs[b]]] < N[10^-ep], 0, Sign[a-b]] 
 ]
];

I have tested the behavior of this mock function with the actual Internal`CompareNumeric over a large range of prec, a b, and they match. (edit 3.4.2017: adjusted the mock function to get the correct behavior for MachinePrecision input.)

Addendum

Ofcourse, the actual Internal`CompareNumeric would not work like this. Instead it probably uses some low level functions working directly on the internal representation of the arbitrary precision numbers. (It certainly is a lot faster) However, the mock function gives us a fairly good idea of the behavior of Internal`CompareNumeric[prec,a,b].

In short it determines some effective precision (ep in the mock function) from prec and the minimal precision of the inputs a and b and then determines whether a > b within a precision tolerance set by ep.

The difference between the behavior of ep dependent on whether the input precision is larger or smaller than machine precision probably arises due to differences in implementation leveraging the fact that for precision smaller than machine precision, Mathematica represents its arbitrary precision numbers simply as a pair of machine numbers representing the value and the precision of the number, in which case it can leverage various machine operations to do the comparison. I suspect that similarly the lower bounds on ep arise some checks that can be down efficiently using low level functions. The scaling of ep when ip < MP presumably is some design choice relating to the desired functionality, possibly related with wanting the effective precision to be larger than zero for reasonable values of prec.