How to illustrate the optimal solution with kinked constraint?

Question

I have a simple optimization problem with a linear, continuous constraint or a kinked constraint. The optimal solution is either a tangent point with f*<T or at the kink with f*=T. The standard illustration is running fine; the illustration of the kinked constraint too.

I am struggling to illustrate the optimal solution with conditions in the manipulate output.

Thank you!

Update 12/7/2020: I reduced the code and added an illustration of the problem's objective.

Clear["Global`*"]
(* Objective function *)
U[f_, c_, a_] := f^a*c^(1 - a);
(* Downward-slope part of constraint )
Bconstr[f_, c_, T_, w_] := c - (T - f)w - n;
(* Kinked Constrained )
Bconstrtransf[f_, c_, T_, w_, n_] = 
  Piecewise[{{c - (T - f)w - n, f < T}}];
(* Optimality Conditions *)
MRS = D[U[f, c, a], f]/D[U[f, c, a], c];
AbsSlpCon = D[Bconstr[f, c, T, w], f];
TC = MRS - AbsSlpCon;
(* Optimal Solution  - either tangency for f<T or f=T )
sols = Solve[{TC == 0, Bconstrtransf[f, c, T, w, n] == 0}, {f, c}][[1,1, 2]];
fcopttransf[T_, w_, a_, n_, f_] := Evaluate[{f, c} /. Last[sols]];
(* Illustration: Optimal Choice with Kinked Constrained - either on downward (point A) or at kink (point B)*)
c1transf[T_, w_, n_, f_] := 
 c /. Solve[Bconstrtransf[f, c, T, w, n] == 0, c][[1]]
vline[T_, w_, n_] := Line[{{T, 0}, {T, n}}]
c2transf[T_, w_, a_, n_, f_] = 
  Quiet[c /. 
    Solve[U[## & @@ fcopttransf[T, w, a, n, f], a] == U[f, c, a], c][[
     1]]];
Manipulate[
 Plot[{c1transf[T, w, n, f], c2transf[T, w, a, n, f]}, {f, 0, 24}, 
  PlotRange -> {{0, 25}, {0, 6000}}, 
  Epilog -> {ColorData[97][1], vline[T, w, n], Red, PointSize@Large, 
    Point@fcopttransf[T, w, a, n, f]}], {{T, 8}, 1, 24, 1, 
  Appearance -> "Labeled"}, {{w, 120}, 10, 200, 5, 
  Appearance -> "Labeled"}, {{n, 500}, 0, 2000, 100, 
  Appearance -> "Labeled"}, {{a, 0.5}, 10^-2, 1, 0.01, 
  Appearance -> "Labeled"}]

Update 12/13/2020: The answer and comments below provide a solution in which the constraint of f<T is not binding and the optimal point is outside the constraint.

In the scenario below, the red dot as optimal solution should not be outside the constraint but at the kink as the constraint dictates f<=T. The tangent curve is also not appearing.

The problem works fine without a piecewise constraint and solutions can be calculated and illustrated - both linear c1 and nonlinear c2.

Answer 1

(*Illustration:Optimal Choice with Standard Constrained*)
c1[T_, w_, f_] := Solve[Bconstr[f, c, T, w] == 0, c][[1, 1, 2]];
c2[T_, w_, a_, f_] = 
 Quiet[c /. Solve[U[## & @@ fcopt[T, w, a], a] == U[f, c, a], c][[1]]];
Manipulate[
 Plot[{c1[T, w, f], c2[T, w, a, f]}, {f, 0, 24}, 
  PlotRange -> {{0, 25}, {0, 6000}}, 
  Epilog -> {Red, PointSize@Large, Point@fcopt[T, w, a]}], {{T, 8}, 1,
   24, 1, Appearance -> "Labeled"}, {{w, 120}, 10, 200, 5, 
  Appearance -> "Labeled"}, {{a, 0.5}, 10^-2, 1, 0.01, 
  Appearance -> "Labeled"}]

works properly.

(Illustration:Kinked Constrained)

c1transf[T_, w_, n_] := 
 Solve[Bconstrtransf[f, c, T, w, n] == 0, c][[1, 1, 2]]
vline[T_, w_, n_] := Line[{{T, 0}, {T, n}}]
(*Illustration:Kinked Constrained*)
c1transf[T_, w_, n_, f_] := 
 c /. Solve[Bconstrtransf[f, c, T, w, n] == 0, c][[1]]
vline[T_, w_, n_] := Line[{{T, 0}, {T, n}}]
Manipulate[
 Plot[c1transf[T, w, n, f], {f, 0, 24}, 
  PlotRange -> {{0, 25}, {0, 6000}}, 
  Epilog -> {ColorData[97][1], vline[T, w, n]}], {{T, 8}, 1, 24, 1, 
  Appearance -> "Labeled"}, {{w, 120}, 10, 200, 5, 
  Appearance -> "Labeled"}, {{n, 500}, 0, 2000, 100, 
  Appearance -> "Labeled"}]

works properly.

(*Optimal Choice:Kinked Constrained-either tangency for f*<T or f* =T*)
sols2 = Solve[{TC == 0, Bconstrtransf[f, c, T, w, n] == 0}, {f, 
     c}][[1, 1, 2]];
fcopttransf[T_, w_, a_, n_, f_] := Evaluate[{f, c} /. Last[sols2]];
(Illustration:Optimal Choice with Kinked Constrained)
c2transf[T_, w_, a_, n_, f_] = 
  Quiet[c /. 
    Solve[U[## & @@ fcopttransf[T, w, a, n, f], a] == U[f, c, a], 
      c][[1]]];

The last Manipulate is really complex. It complains about solutions in this form

Manipulate[
 Plot[{c1transf[T, w, n, f], c2transf[T, w, a, n, f]}, {f, 0, 24}, 
  PlotRange -> {{0, 25}, {0, 6000}}, 
  Epilog -> {ColorData[97][1], vline[T, w, n], Red, PointSize@Large, 
    Point@fcopttransf[T, w, a, n, f]}], {{T, 8}, 1, 24, 1, 
  Appearance -> "Labeled"}, {{w, 120}, 10, 200, 5, 
  Appearance -> "Labeled"}, {{n, 500}, 0, 2000, 100, 
  Appearance -> "Labeled"}, {{a, 0.5}, 10^-2, 1, 0.01, 
  Appearance -> "Labeled"}]

That repairs the misconceptions on the level of variables, parameters. I replaced rules by the corresponding part. For last manipulate this is an improvement. I did not prefer to correct the implemented logic and semantics. It is now in the c2transf function that problems occur. I am the opinion the question "I am struggling to illustrate the optimal solution with conditions in the manipulate output." is done by that effort.

I suggest to make use of ideas from this demonstration: PhysicsOfASlidingLadder.

I shortened it so that it works: (Optimal Solution-either tangency for f<T or f=T*)

fcopttransf[T_, w_, a_, n_, f_] := Solve[a c - w*((1 - a) f) == 0 && c - (T - f)*w - n == 0, {f, c}][[1, All, 2]]

(Illustration:Optimal Choice with Kinked Constrained-either on
downward (point A) or at kink (point B))

c1transf[T_, w_, n_, f_] := n - f w + T w vline[T_, w_, n_] := Line[{{T, 0}, {T, n}}]

c2transf[T_, w_, a_, n_, f_] = Quiet[Solve[(-1)^a (1/w)^(1 - a) == f^a*c^(1 - a) && f < T && f < T, c][[1, 1, 2]]];

Manipulate[
 Plot[{c1transf[T, w, n, f], c2transf[T, w, a, n, f]}, {f, 0, T}, 
  PlotRange -> {{0, 25}, {0, 6000}}, 
  Epilog -> {ColorData[97][1], vline[T, w, n], Red, PointSize@Large, 
    Point@fcopttransf[T, w, a, n, f]}], {{T, 8}, 1, 24, 1, 
  Appearance -> "Labeled"}, {{w, 120}, 10, 200, 5, 
  Appearance -> "Labeled"}, {{n, 500}, 0, 2000, 100, 
  Appearance -> "Labeled"}, {{a, 0.5}, 10^-2, 1, 0.01, 
  Appearance -> "Labeled"}]

The trick is given in this post by @leonid-shifrin: performance tuning in Mathematica: "Avoid full Mathematica symbolic evaluation process as much as possible.". @leonid-shifrin points out that even compiled functions of Your type may bail out into being not fast and keep causing trouble.

With[{T = 20, w = 5, n = 2, c = 1, f = 2}, 
 Plot[{Re[(-1)^a (1/w)^(1 - a)], f^a*c^(1 - a), 
   c2transf[T, w, a, n, f]}, {a, 0, 1}, PlotRange -> Full, 
  PlotLegends -> "Expressions"]]

There are only single points where a solution exists:

Plot[{Re[(-1)^a (1/5)^(1 - a)], .1^a*1^(1 - a), 
  c2transf[20, 5, a, 2, 2]}, {a, 0, 2.6}, PlotRange -> Full, 
 PlotLegends -> "Expressions"]

Based on the number of parameters this can only be solved to examples. This already makes use of the Mathematica definition of Re.

Have fun.

OK. I see I have to change the syntactics.

This is not so a nice problem to be solves with FindRoot. Graphical is much more appropriate to gain understanding and routine. How to built this last part.

Do try to understand this code:

Manipulate[
 Show[Graphics[{PointSize[Large], 
    Point[{f1, (A ((f1 - c1)^-a))^(1/1 - a)}], 
    Point[{f2, (B ((f2 - c2)^-b))^(1/1 - b)}], {Dashed, 
     Line[{{f2, 0}, {f2, (B ((f2 - c2)^-b))^(1/1 - b)}}], 
     Line[{{f1, 0}, {f1, (A ((f1 - c1)^-a))^(1/1 - a)}}], 
     Line[{{0, (B ((f2 - c2)^-b))^(1/1 - 
           b)}, {f2, (B ((f2 - c2)^-b))^(1/1 - b)}}], 
     Line[{{0, (A ((f1 - c1)^-a))^(1/1 - 
           a)}, {f1, (A ((f1 - c1)^-a))^(1/1 - a)}}]}, 
    Arrow[{{S, 0}, {TT, 0}}], Arrow[{{0, U}, {0, V}}], 
    Inset["c", {-0.2, (B ((f2 - c2)^-b))^(1/1 - b)}], 
    Inset["c*", {-0.2, (A ((f1 - c1)^-a))^(1/1 - a)}], 
    Inset["f2", {f2, -0.2}], Inset["f1", {f1, -0.2}], 
    Inset["f", {TT, -0.2}], Inset["c", {-0.2, V}]}], 
  Plot[{Labeled[(A ((f - c1)^-a))^(1/1 - a), A f^a], 
    Labeled[(B ((f - c2)^-b))^(1/1 - b), B f^b], 
    Piecewise[{{(B ((f2 - c2)^-b))^(1/1 - b) + (f - f2) (-1 + 
           b) b B f2^(-1 - b) (c2 + B f2^-b)^-b, f < f1}, {0, 
       f == f1}, {Nothing, f > f1}}]}, {f, S, TT}, PlotPoints -> 25, 
   PlotRange -> {{S, TT}, {U, V}}, AxesLabel -> {f, c}, Ticks -> tcks,
    Epilog -> {}]], {{a, 0.5}, 0.01, 1 - 0.00001, 
  Appearance -> "Labeled"}, {{b, 0.6}, 0.01, 1 - 0.000001, 
  Appearance -> "Labeled"}, {{A, 1.47}, 0.1, 10, 
  Appearance -> "Labeled"}, {{B, 1}, 0.1, 10, 
  Appearance -> "Labeled"}, {{c1, 0.1}, 0.1, 1.5, 
  Appearance -> "Labeled"}, {{c2, 0.2}, 0.1, 1.6, 
  Appearance -> "Labeled"}, {{S, 0.0001}, 0.000001, 2, 
  Appearance -> "Labeled"}, {{TT, 6}, 0.1, 7, 
  Appearance -> "Labeled"}, {{U, 0.01}, 0, 10, 
  Appearance -> "Labeled"}, {{V, 5}, 0.1, 10, 
  Appearance -> "Labeled"}, {{f1, 0.6}, 0.01, 3, 
  Appearance -> "Labeled"}, {{f2, 0.4}, 0.01, 3, 
  Appearance -> "Labeled"}]

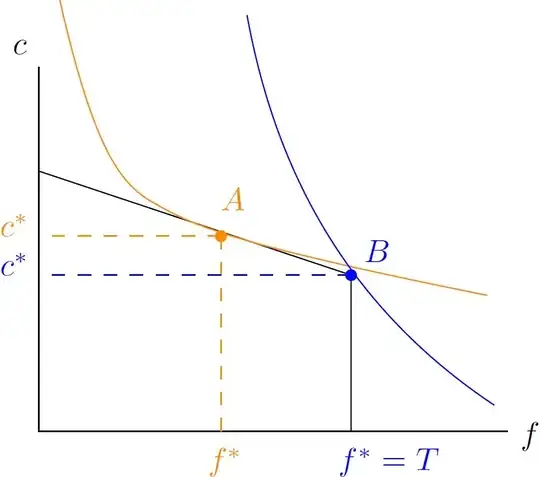
The code is for exploration and learning purposes only. It offers nevertheless a graphical full fledged Mathematica Manipulate for solving the problem displayed in the questions picture.

Would I attempt to solve this with a FindRoot it would fail. The final problem would be

Solve[(B (f2^-b) + c2)^(1/1 - b) + (f - f2) (-1 + b) b B f2^(-1 - 
     b) (c2 + B f2^-b)^-b == (A ((f - c1)^-a))^(1/1 - a), f]

or FindRoot, Reduce or else Mathematica solving built-in. The problem can be tackled with more effort. It is necessary to transfer the constrains from the introductory Manipulate into the built-in selected finally for determining a solution. That is again in the range of the effort done for the Manipulate.

This is long and tedious. This does not avoid possible singularities, domains. It is a start that works. It requires to set up an own strategy how to reach an point induced by the picture of the question. It requires to name the parameters. There is still some difference to the pictures. But it is much further develop then the code from the original question.

It avoids complete what the solution of the question with the code targeted. This is in difference to the original question a problem of the type Exponentiation or Power. It is oriented to isentropic processes from ideal gases. It simply adds the linear tangent to the power curve and lets the point to manipulation. This offers insight and demands the effort of gaining experience first.

It confines the problem close to given graphics and gives only some basic idea that can be used to proceed further to the graphics in the manner of a framework for such tasks. It does not confine the ranges at all. It does not avoid singularities of the used inverse functions nor does it solve the problem overall. It is just a graphical approach to solutions in the open experimental fashion that Mathematica Manipulate induces.

There many pedagogical questions open. But one should be cleared locality triumph over $FindRoot$ global attempting.