The function hermiteToBezierPoints[] computes the Bezier control points for BezierCurve from values of the function and its derivatives up to some order at each endpoint of an interval.
The function ifnToBezierCurve[ifn] passes the relevant data for an interpolating function ifn to hermiteToBezierPoints[] and wraps the results in BezierCurve or JoinedCurve[BezierCurve[...],...].
I originally started down this line of development when I read this Q&A:
Plot with NDSolve for a range of initial values.
So the motivation was to plot NDSolve solutions via Bezier curves.
The function ifnToBezierCurve[] might convert any univariate scalar-valued InterpolatingFunction, although it complains about those that do not have "Hermite" as the "InterpolationMethod". I had to guess what InterpolatingFunction does when the function data at the end points is insufficient to determine an interpolant of degree InterpolationOrder. These are the ones that can have kinks. It uses data from adjacent points, but I had to guess exactly how. So far it has worked on the random examples I threw at it. It handles ones that have jump discontinuities with a simple application of Split[..., Unequal] and Internal`PartitionRagged.
Examples
OP's.
ifn = NDSolveValue[{y''[x] + y[x]^3 == 0, y[0] == 1, y'[0] == 0},
y, {x, 0, 10}, Method -> "Extrapolation"];
Show[
ListLinePlot[ifn, PlotStyle -> AbsoluteThickness[4.6]],
Graphics[{
ColorData[97][2], AbsoluteThickness[2.6],
ifnToBezierCurve[ifn]
}]
]

Developer`PackedArrayForm of order 3
ifnToBezierCurve[
NDSolveValue[{y''[x] + y[x]^3 == 0, y[0] == 1, y'[0] == 0},
y, {x, 0, 1}]] // Graphics
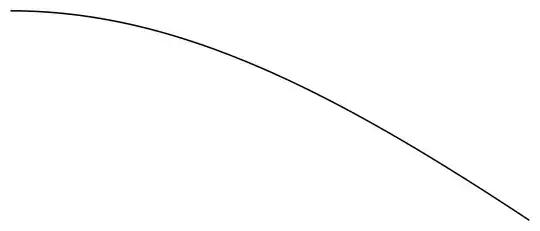
Variable order, non-Hermite method. Graphics output same as above.
ifnToBezierCurve[
NDSolveValue[{y''[x] + y[x]^3 == 0, y[0] == 1, y'[0] == 0},
y, {x, 0, 1}, InterpolationOrder -> All]] // Graphics
ifnToBezierCurve::meth: Currently converting interpolations using interpolation method Local Taylor series are unimplemented; returning a BezierCurve based on Hermite method with SplineDegree -> 3.
You can override the warning by explicitly setting SplineDegree, which then creates Bezier curves of uniform degree from the interpolating function and its derivatives. (Graphics same as above.)
ifnToBezierCurve[
NDSolveValue[{y''[x] + y[x]^3 == 0, y[0] == 1, y'[0] == 0},
y, {x, 0, 1}, InterpolationOrder -> All],
SplineDegree -> 5] // Graphics
Discontinuities
Here's an ODE that has jumps:
Graphics[{
ifnToBezierCurve[
NDSolveValue[{y'[x] + y[x] ==
2 DiracDelta[x - 1] + 2 DiracDelta[x - 2] + 2 DiracDelta[x - 3],
y[0] == 1}, y, {x, 0, 4}]]
},
PlotRange -> All,
Options@Plot]
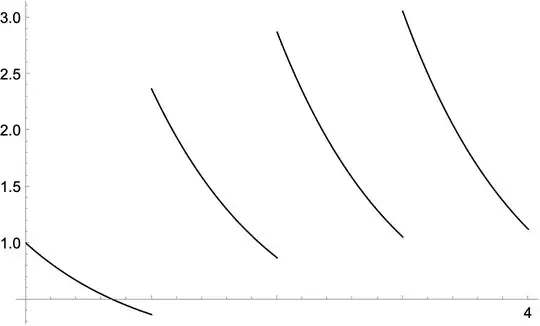
Irregular, user-defined interpolation with kinks
idata = {{{0}, 1, 2, -1}, {{1}, -1}, {{3/2}, 1}, {{2}, 3}, {{5/2},
0}, {{3}, -1, 1, 2, -3, 1}};
foo = Interpolation[N@idata, InterpolationOrder -> 4];
Show[
Plot[foo[t], {t, 0, 3}, PlotStyle -> AbsoluteThickness[5.6],
PlotRange -> All],
Graphics[{ColorData[97][2], AbsoluteThickness[2.6],
ifnToBezierCurve@foo
}]
]
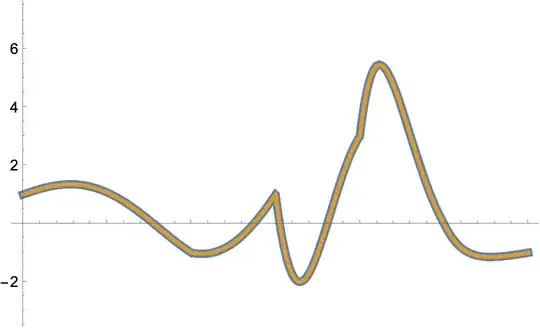
Code dump
(* Bezier pts from derivatives at x0, x1 *)
hermiteToBezierPoints // ClearAll;
hermiteToBezierPoints[{{x0_}, f0__}, {{x1_}, f1__}] :=
hermiteToBezierPoints[{x0, x1}, {f0}, {f1}];
hermiteToBezierPoints[{x0_, x1_}, f0_?VectorQ, f1_?VectorQ] :=
Module[
{dx, order0, rng0, order1, rng1, n, yy0, yy1},
dx = x1 - x0;
order0 = Length@f0 - 1;
rng0 = Range[0, order0];
order1 = Length@f1 - 1;
rng1 = Range[0, order1];
n = order0 + order1 + 1;(* Bezier/Hermite order *)
yy0 = f0*dx^rng0/Pochhammer[n + 1 - rng0, rng0];
yy1 = f1*(-dx)^rng1/Pochhammer[n + 1 - rng1, rng1];
Transpose@{
Subdivide[x0, x1, n],
Join[
Outer[Binomial, rng0, rng0] . yy0,
Outer[Binomial, rng1, rng1] . yy1 // Reverse]
}
];
(*"
- Single BezierCurve per segment alternative
"*)
(* unneeded as yet
(bit field positions-inferred,perhaps mistaken)
$bitFlagsPos=2;
$extrapBit=0;(whether to warn about extrapolation)
$rectArrayBit=1; (whether the data (f,f',...) is a rectangular array
(not ragged) )
$machPrecBit=2; (whether the data (f,f',...) is MachinePrecision )
$repeatedBit=4; (whether repeated abscissae are permitted )
*)
ifnGetData // ClearAll;
iIfnGetData // ClearAll;
(*** internal function *)
iIfnGetData[
if : Verbatim[InterpolatingFunction][, type,
coords_, {Developer`PackedArrayForm, split_, a_}, ___],
Automatic] /; if["InterpolationMethod"] === "Hermite"(/;BitAnd[
type[[$bitFlagsPos]],2^$rectArrayBit]>0):=
<|"Coordinates" -> coords,
"FunctionData" ->
Internal`PartitionRagged[a, Differences@split]|>;
iIfnGetData[
if : Verbatim[InterpolatingFunction][, type, coords_,
a : {__List}, ___], Automatic] /;
if["InterpolationMethod"] === "Hermite" :=
<|"Coordinates" -> coords,
"FunctionData" -> a|>;
(* non-Hermite )
iIfnGetData[if_InterpolatingFunction, Automatic] /;
if["InterpolationMethod"] =!= "Hermite" := (
Message[ifnToBezierCurve::meth, if["InterpolationMethod"],
First@if["InterpolationOrder"]];
iIfnGetData[if, First@if["InterpolationOrder"]]);
( non-Automatic SplineDegree )
iIfnGetData[if_InterpolatingFunction, sdeg_Integer?Positive] :=
( SplineDegree deg will be effectively be odd *)
With[{coords = if@"Coordinates",
a = Transpose@
Through[NestList[Derivative[1], if, Floor[sdeg/2]][
"ValuesOnGrid"]]},
<|"Coordinates" -> coords,
"FunctionData" -> a|>
];
(* UI function ***)
ifnGetData[if_InterpolatingFunction, sdeg_] :=
Module[{data},
data = iIfnGetData[if, sdeg];
With[{coordsegs = Split[First@data@"Coordinates", Unequal]},
{coordsegs,
Internal`PartitionRagged[data@"FunctionData",
Length /@ coordsegs]}
]];
ifnToBezierCurve // ClearAll;
ifnToBezierCurve::meth =
"Currently converting interpolations using interpolation method \ are unimplemented; returning a BezierCurve based on Hermite method \ with SplineDegree ->.";
(* If SplineDegree is not Automatic then Hermite interpolation model
is used )
ifnToBezierCurve // Options = {SplineDegree -> Automatic};
ifnToBezierCurve[ifn_InterpolatingFunction, OptionsPattern[]] /;
Length@ifn@"Domain" == 1 && ifn@"OutputDimensions" === {} :=
With[{data = ifnGetData[ifn, OptionValue@SplineDegree]},
MapThread[
Function[{t, x},( time steps, function step data )
If[
MatrixQ[x] &&
2 Length@x[[1]] > First@ifn@"InterpolationOrder",
( all components the same sufficient degree )
With[{sd = 2 Length@x[[1]] - 1},( SplineDegree )
BezierCurve[ ( composite BezierCurve )
Join[
{{t[[1]], x[[1, 1]]}},
Flatten[
MapThread[
Rest[hermiteToBezierPoints[##]] &,
{Partition[t, 2, 1], Most[x], Rest[x]}
],
1]
],
SplineDegree -> sd]
],
( degrees of components vary or
are less than InterpolatingOrder )
Module[{delayedRest, iorder, ncoeffs, i},
delayedRest := (delayedRest = Rest; Identity);
ncoeffs = Length /@ x;
JoinedCurve@ ( joined BezierCurve pieces )
Table[
iorder = ncoeffs[[j]] + ncoeffs[[j + 1]] - 1;
i = 0;
While[iorder < First@ifn@"InterpolationOrder",
++i;
With[{dj = 3/4 - 1/4 (-1)^i (3 + 2 i)},
If[1 <= j + dj <= Length@x,
iorder += ncoeffs[[j + dj]]
]]
];
With[{bpts = hermiteToBezierPoints[
{t[[j]], t[[j + 1]]},
x[[j]],
Join[
x[[j + 1]],
Table[Derivative[k][ifn][t[[j + 1]]],
{k, ncoeffs[[j + 1]], iorder - ncoeffs[[j]]}]]
]},
BezierCurve[delayedRest@bpts,
SplineDegree -> Length[bpts] - 1]
],
{j, Length@t - 1}
]]
] ( end If[] *)
],
data
] /; FreeQ[data, ifnGetData]
];




