How to display the support $\mathrm{supp}(f)$ of a piecewise function $z = f(x,y)$?

Question

I'm wondering how to display the support $\mathrm{supp}(f)$ of a piecewise surface $z = f(x,y)$.

As an example, let's consider the following piecewise function (and plot it):

f[x_, y_] = Piecewise[{{1, 0 <= x <= 1 && 0 <= y <= 1}}];
g[x_, y_] = Integrate[f[x - t, y - t], {t, 0, 1}];
Plot3D[g[x, y], {x, -0.5, 2.5}, {y, -0.5, 2.5}, PlotRange -> Full]

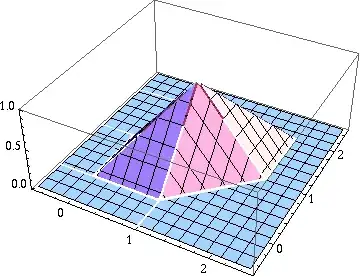
My first thought was to use a contour plot for this purpose, such as

ContourPlot[g[x, y] == .05, {x, -0.5, 2.5}, {y, -0.5, 2.5}]

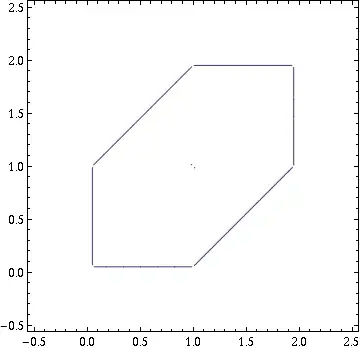
But this is of course only an approximation of the support. How do I display the actual support of my piecewise function?

Edit

The proposed solution in the comments below works great, the result looks as follows:

Answer 1

Here's another quick way to visualize the support region:

RegionPlot[Or @@ g[x, y][[1, All, 2]] // Evaluate, {x, -0.5, 2.5}, {y, -0.5, 2.5}]

.

In some cases, one might want to run Reduce[] on the pile of constraints produced by Or @@ g[x, y][[1, All, 2]], before plotting, to reduce evaluation effort. (In this case, it did not do much, but it's a good idea in general.)

If one is not afraid of undocumented functions, here is another method:

RegionPlot[Or @@ Most[First[Internal`FromPiecewise[g[x, y]]]] // Evaluate,
           {x, -0.5, 2.5}, {y, -0.5, 2.5}]

Answer 2

The most direct way uses RegionPlot e.g.

RegionPlot[ g[x, y] > 0, {x, -0.5, 2.5}, {y, -0.5, 2.5}]

let's customize it a bit using colors from many possible ColorData["Gradients"]:

GraphicsRow[ 
    RegionPlot[ g[x, y] > 0, {x, -0.5, 2.5}, {y, -0.5, 2.5}, 
                ColorFunction -> Function[{x, y}, ColorData[#][Abs[g[x, y]]]], 
                ColorFunctionScaling -> False, PlotPoints -> 100, MaxRecursion -> 5]& /@
    {"BlueGreenYellow", "DarkBands"} ]

One can also get the plot with ContourPlot, e.g. using the RegionFunction option:

ContourPlot[ g[x, y], {x, -0.5, 2.5}, {y, -0.5, 2.5}, 
             RegionFunction -> Function[{x, y}, g[x, y] > 0], Exclusions -> None] 

At last, we can make Plot3D better fitting to our needs:

Plot3D[ g[x, y], {x, -0.5, 2.5}, {y, -0.5, 2.5}, MeshFunctions -> {#3 &}, 
        PlotRange -> All, RegionFunction -> Function[{x, y}, g[x, y] > 0], 
        ColorFunction -> Function[{x, y}, ColorData["BlueGreenYellow"][g[x, y]]], 
        ColorFunctionScaling -> False, BoxRatios -> {2, 2, 1}, PlotPoints -> 80, 
        MaxRecursion -> 4, Exclusions -> None]