I'd like to display field lines for a point charge in 3 dimensions. Not a force field (short arrows) but continuous field lines that start on the charge.
-
3I think he's looking for a 3D version of StreamPlot. – David Jan 25 '12 at 22:07
-
@David I was just coming to the same conclusion. That's a good question. (+1) – Mr.Wizard Jan 25 '12 at 22:09
-
@David seems so. – acl Jan 25 '12 at 22:19
-
2Michael Trott gives some code for visualizing field lines of charges in his book. I can transcribe it if needed. – J. M.'s missing motivation Jan 25 '12 at 22:44
-
Hello Rainforest Frog and welcome to the Mathematica StackExchange. Don't forget to upvote good answers (and other people's questions) using the triangle above the number next to the post, and use the checkmark to "accept" the answer to your question that you think best answers it. You now have enough "reputation" (points) to visit the chat room and chat if you would like. – Verbeia Jan 25 '12 at 22:45
-
2@Ruslan Thanks for the nice comment! – Jens Feb 06 '15 at 18:47
3 Answers
This is something I have used for my classes. Over time, I've tried to make it more and more user friendly, but that's also made it a little longish. I'll post the complete set of functions, with apologies if it's a bit unwieldy...
As you'll see, I found it does indeed work better in my use cases if I normalize the field, so that we advance along the field lines in more balanced steps. The hardest part in applying these functions is to choose the appropriate seed points.
fieldSolve::usage =
"fieldSolve[f,x,x0,\!\(\*SubscriptBox[\(t\), \(max\)]\)] \
symbolically takes a vector field f with respect to the vector \
variable x, and then finds a vector curve r[t] starting at the point \
x0 satisfying the equation dr/dt=\[Alpha] f[r[t]] for \
t=0...\!\(\*SubscriptBox[\(t\), \(max\)]\). Here \[Alpha]=1/|f[r[t]]| \
for normalization. To get verbose output add debug=True to the \
parameter list.";
fieldSolve[field_, varlist_, xi0_, tmax_, debug_: False] := Module[
{xiVec, equationSet, t},
If[Length[varlist] != Length[xi0],
Print["Number of variables must equal number of initial conditions\
\nUSAGE:\n" <> fieldSolve::usage]; Abort[]];
xiVec = Through[varlist[t]];
(* Below, Simplify[equationSet] would cost extra time
and doesn't help with the numerical solution, so don't try to simplify. *)
equationSet = Join[
Thread[
Map[D[#, t] &, xiVec] ==
Normalize[field /. Thread[varlist -> xiVec]]
],
Thread[
(xiVec /. t -> 0) == xi0
]
];
If[debug,
Print[Row[{"Numerically solving the system of equations\n\n",
TraditionalForm[(Simplify[equationSet] /. t -> "t") //
TableForm]}]]];
(* This is where the differential equation is solved.
The Quiet[] command suppresses warning messages because numerical precision isn't crucial for our plotting purposes: *)
Map[Head, First[xiVec /.
Quiet[NDSolve[
equationSet,
xiVec,
{t, 0, tmax}
]]], 2]
]
fieldLinePlot[field_, varList_, seedList_, opts : OptionsPattern[]] :=
Module[{sols, localVars, var, localField, plotOptions,
tubeFunction, tubePlotStyle, postProcess = {}},
plotOptions = FilterRules[{opts}, Options[ParametricPlot3D]];
tubeFunction = OptionValue["TubeFunction"];
If[tubeFunction =!= None,
tubePlotStyle = Cases[OptionValue[PlotStyle], Except[_Tube]];
plotOptions =
FilterRules[plotOptions,
Except[{PlotStyle, ColorFunction, ColorFunctionScaling}]];
postProcess =
Line[x_] :>
Join[tubePlotStyle, {CapForm["Butt"],
Tube[x, tubeFunction @@@ x]}]
];
If[Length[seedList[[1, 1]]] != Length[varList],
Print["Number of variables must equal number of initial \
conditions\nUSAGE:\n" <> fieldLinePlot::usage]; Abort[]];
localVars = Array[var, Length[varList]];
localField =
ReleaseHold[
Hold[field] /.
Thread[Map[HoldPattern, Unevaluated[varList]] -> localVars]];
(*Assume that each element of seedList specifies a point AND the \
length of the field line:*)Show[
ParallelTable[
ParametricPlot3D[
Evaluate[
Through[#[t]]], {t, #[[1, 1, 1, 1]], #[[1, 1, 1, 2]]},
Evaluate@Apply[Sequence, plotOptions]
] &[fieldSolve[
localField, localVars, seedList[[i, 1]], seedList[[i, 2]]
]
] /. postProcess, {i, Length[seedList]}
]
]
];
Options[fieldLinePlot] =
Append[Options[ParametricPlot3D], "TubeFunction" -> None];
SyntaxInformation[fieldLinePlot] = {"LocalVariables" -> {"Solve", {2, 2}},
"ArgumentsPattern" -> {_, _, _, OptionsPattern[]}};
SetAttributes[fieldSolve, HoldAll];
The main function is fieldLinePlot, but I split it into two functions to be more modular. Also, the problem of where to start drawing the field lines is treated separately because it depends a lot on the particular application.
fieldSolve[f,x,x0,Subscript[t, max]] symbolically takes a vector field f with respect to the vector variable x, and then finds a vector curve r[t] starting at the point x0 satisfying the equation dr/dt = α f[r[t]] for t=0...tmax. Here α = 1/|f[r[t]]| for normalization. To get verbose output add debug=True to the parameter list.
fieldLinePlot[field,varlist,seedList] plots 3D field lines of a vector field (first argument) that depends on the symbolic variables in varlist. The starting points for these variables are provided in seedList.
Each element of seedList={{p1, T1},{p2, T2}...} is a tuple where pi is the starting point of the $i^\mathrm{th}$ field line and Ti is the length of that field line in both directions from Pi.
Here are some examples:
1) Coulomb field of two opposite charges at $\vec{r} = \vec{0}$ and $\vec{r} = (1, 1, 1)$:
Look at the form of seedList to see how the field line starting points and lengths are specified.
seedList =
With[{vertices = .1 N[PolyhedronData["Icosahedron"][[1, 1]]]},
Join[Map[{#, 2} &, vertices],
Map[{# + {1, 1, 1}, -2} &, vertices]]];
Show[fieldLinePlot[{x, y, z}/
Norm[{x, y, z}]^3 - ({x, y, z} - {1, 1, 1})/
Norm[{x, y, z} - {1, 1, 1}]^3, {x, y, z}, seedList,
PlotStyle -> {Orange, Specularity[White, 16], Tube[.01]},
PlotRange -> All, Boxed -> False, Axes -> None],
Background -> Black]

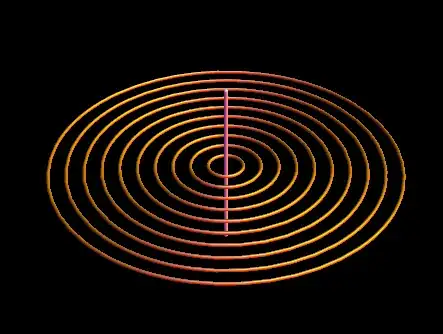
2) Magnetic field of an infinite straight wire:
With[{seedList = Table[{{x, 0, 0}, 6.5}, {x, .1, 1, .1}]
},
Show[fieldLinePlot[{-y, x, 0}/(x^2 + y^2), {x, y, z},
seedList, PlotStyle -> {Orange, Specularity[White, 16], Tube[.01]},
PlotRange -> All, Boxed -> False, Axes -> None],
Graphics3D@Tube[{{0, 0, -.5}, {0, 0, .5}}], Background -> Black]]
Edit: added variable line thickness to represent field strength
The field lines can be given a color that scales with the field strength (the norm of the vector field along the lines), by specifying a ColorFunction in fieldLinePlot. For example, if the vector field has been defined as a function f2 of variables x,y,z, then you could add the option ColorFunctionScaling -> False, ColorFunction -> Function[{x,y,z,u}, Quiet@Hue[Clip[ Norm[f2[x,y,z]],{0,20}]/20]] as I mention in the comment section.
In this new edit, I added the ability to encode the field strength in the thickness of the field lines instead. This required adding a new option "TubeFunction" which works similarly to ColorFunction. It is a function of the three coordinates x,y,z and returns the radius of the tube representing the field line at that point. To calculate this radius in the examples below, I take the (unscaled) value of the field and get its Norm. Then I scale and constrain it to a reasonable range so that the thickness variations of the field lines don't look too grotesque:
3) Same Coulomb field as above, but with varying field line thickness
f2[x_, y_,z_] := {x, y, z}/Norm[{x, y, z}]^3 - ({x, y, z} - {1, 1, 1})/
Norm[{x, y, z} - {1, 1, 1}]^3
seedList =
With[{vertices = .1 N[PolyhedronData["Icosahedron"][[1, 1]]]},
Join[Map[{#, 2} &, vertices],
Map[{# + {1, 1, 1}, -2} &, vertices]]];
fieldLinePlot[f2[x, y, z], {x, y, z}, seedList,
PlotStyle -> {Orange, Specularity[White, 16]}, PlotRange -> All,
Boxed -> False, Axes -> None,
"TubeFunction" ->
Function[{x, y, z}, Quiet[Clip[Norm[f2[x, y, z]], {2, 40}]/200]],
Background -> Black]

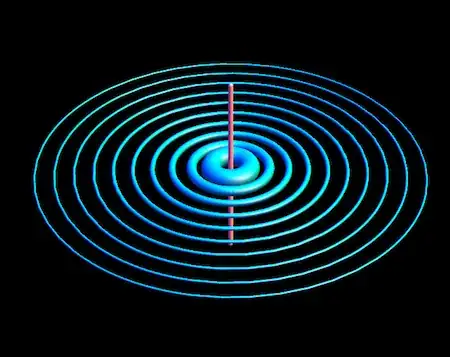
4) Same magnetic field as above, this time with varying line thickness
f3[x_, y_, z_] := {-y, x, 0}/(x^2 + y^2)
With[{seedList = Table[{{x, 0, 0}, 6.5}, {x, .1, 1, .1}]},
Show[fieldLinePlot[f3[x, y, z], {x, y, z}, seedList,
PlotStyle -> {Cyan, Specularity[White, 16]}, PlotRange -> All,
Boxed -> False, Axes -> None,
"TubeFunction" ->
Function[{x, y, z}, Quiet[Clip[Norm[f3[x, y, z]], {1, 40}]/200]]],
Graphics3D@Tube[{{0, 0, -.5}, {0, 0, .5}}], Background -> Black]]
- 97,245
- 7
- 213
- 499
-
BTW, is there any simple way to change thickness of the tube depending on field strength? – Ruslan Feb 08 '15 at 14:17
-
1@Ruslan That would take some modifications. But you can already display the field strength by using colors, without any modifications to the current code. Just use it with some additional options. E.g., for the Coulomb field, define it as a function
f2[x_,y_,z]and then add this to thefieldLinePlot:ColorFunctionScaling -> False, ColorFunction -> Function[{x,y,z,u}, Quiet@Hue[Clip[ Norm[f2[x,y,z]],{0,20}]/20]]The factor20determines the cutoff for coloring near singularities. If the thickness were used for field strength, it would look very thick near the charges... – Jens Feb 08 '15 at 17:50 -
Of course, I meant that the thickness would have a maximum like clipping does in your color suggestion. – Ruslan Feb 08 '15 at 18:48
-
As for the colouring, I think more understandable would be to use
GrayLevel[1-#]&instead ofHue. – Ruslan Feb 08 '15 at 18:53 -
@Ruslan Sure, that's up to anyone's taste. I may have time to do some modifications regarding thickness later... it's doable but not straightforward, unfortunately. The
Tubecommand lets you adjust the thickness along the curve, butParametricPlot(which I rely on) doesn't utilize that capability (for 1D curves). – Jens Feb 08 '15 at 18:55 -
1
-
Thanks, that looks great. But for some reason it uses a huge amount of RAM and goes into heavy swapping on my machine with 4G of RAM. – Ruslan Feb 09 '15 at 09:46
-
1@Ruslan I tried to be as efficient as possible in terms of graphics, so I would blame the rest on Mathematica - in terms of efficiency and speed, it can't compete with dedicated 3D visualization software. However, one can always build complex 3D scenes in Mathematica by doing it in smaller chunks and combining them with
Showlater. You could try that by doing chunks with smaller lists of seed points and combining them only at the end. As in:seedList[[1;;5]],seedList[[6;;10]], etc. for the argument offieldLinePlot. – Jens Feb 09 '15 at 17:23
Assuming that the motion of the particle is governed by some force field, you could use NDSolve together with ParametricPlot3D to plot the individual field lines. For example, consider the force field
force[p_] := ({1, 1, 1} - p)/Norm[{1, 1, 1} - p]^3 - p/Norm[p]^3
The equations of motion are given by
p[t_] := {p1[t], p2[t], p3[t]}
eqs := Thread[p''[t] == force[p[t]]]
We also need some initial conditions, for example
ic := {Thread[p[0] == {1, 0, 0}], Thread[p'[0] == {0, 1, 0}]}
The system can then be solved according to
sol = NDSolve[{eqs, ic}, {p1, p2, p3}, {t, 0, 20}]
And the plot of this solution looks like
ParametricPlot3D[p[t] /. sol, {t, 0, 20}]
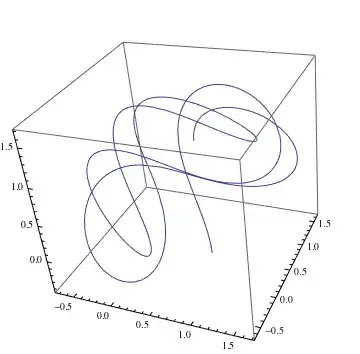
If you want several field lines, you would need to rerun NDSolve for a list of initial conditions.
Edit
As rcollyer pointed out, this doesn't actually plot the field lines. For that you would need to solve p'[t] == force[p[t]]/Norm[force[p[t]] for which you can still use the method above, e.g.
eq := Thread[p'[t] == -force[p[t]]/Sqrt[force[p[t]].force[p[t]]]]
(* seeds for field lines *)
seeds = Flatten[{0.1 #, 0.1 # + {1, 1, 1}} & /@
N[PolyhedronData["Icosahedron"][[1, 1]]], 1];
sol = NDSolve[{eq, Thread[p[0] == #]}, {p1, p2, p3}, {t, 0, 40}][[1]] & /@ seeds;
ParametricPlot3D[p[s] /. sol, {s, 0, 20},
PlotRange -> {{-3, 3}, {-3, 3}, {-3, 3}}]
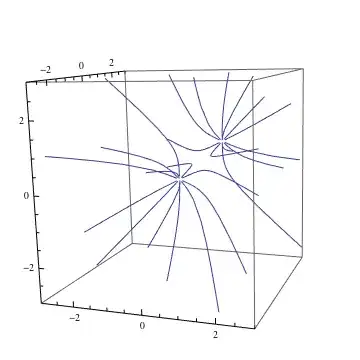
- 35,858
- 3
- 108
- 157
-
You can get the coordinates of the polyhedron easier (and more readable) by using the built-in parameter
VertexCoordinates(... /@ PolyhedronData["Icosahedron", "VertexCoordinates"] ...). – David Jan 26 '12 at 04:29 -
One more thing, the field lines are the integral curves of the vector field, i.e. solutions of $p'(t) = X(p(t))$, there is no division by a norm. (This equation holds on any differentiable manifold, and most of them don't even have a norm.) – David Jan 26 '12 at 04:43
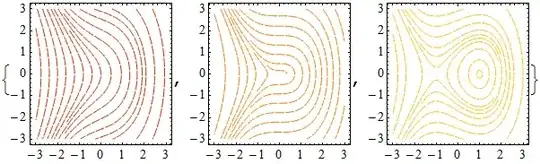
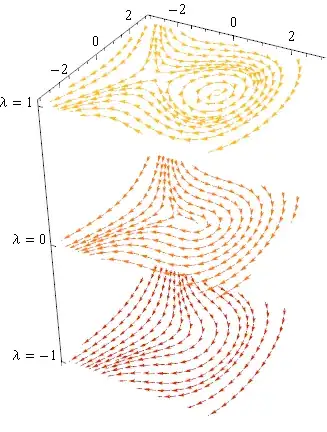
The closest thing in the help files that I can see is this example. It might be of some use.
stackPlots[plots2D : {__Graphics},
dh_, o : OptionsPattern[Graphics3D]] := Graphics3D[
MapIndexed[
Function[{g, index}, g[[1]] /. Arrow[v2d_] :> Arrow[v2d /.
{x_?NumericQ, y_?NumericQ} :> {x, y, dh index[[1]]}]],
plots2D], o]
plotSpacing = 5;
values = {-1, 0, 1};
plots = MapIndexed[
Function[{\[Lambda], i},
StreamPlot[{y, \[Lambda] - x^2}, {x, -3, 3}, {y, -3, 3},
StreamPoints -> 16, StreamScale -> 0.07,
StreamStyle -> ColorData["SolarColors"][0.3 i[[1]]]]], values]
stackPlots[plots, plotSpacing, Axes -> True, Boxed -> False,
Ticks -> {Automatic, Automatic,
MapIndexed[{plotSpacing #2[[1]], Row[{"\[Lambda] = ", #1}]} &,
values]}]