Self-intersecting path of stacked regular tetrahedra

Question

(This question occurred to me after reading @IanAgol's reminisces of Conway's spiral tetrahedron billiard path.)

Let $T_i$ be a regular tetrahedron, and $P$ a collection of regular tetrahedra glued together face-to-face. Say that $P$ constitutes a "path of stacked regular tetrahedra" iff two conditions hold:

1. The dual graph (node for each $T_i$, arc if $T_i$ shares a face with $T_j$) is a path.
2. No edge of the construction is incident to more than three tetrahedra.

The first condition intuitively insists on a snake-like object. The second condition excludes too many tetrahedra circling about one edge. (Without this, $5$ dihedral angles of $70.5^\circ$ fit into $360^\circ$, but $6$ do not.)

My question is:

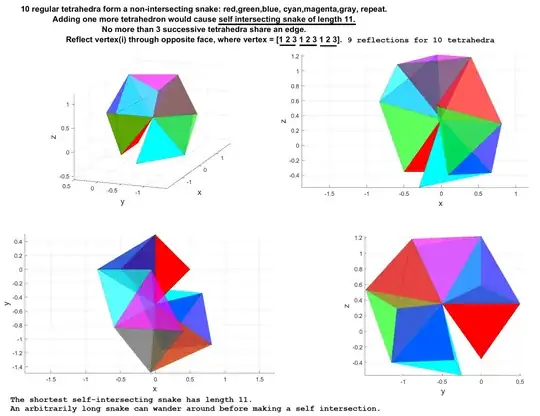
Q. What is the fewest number of tetrahedra in a path $P$ of stacked regular tetrahedra that self-intersects?

$P = \cup_i T_i$ self intersects if a pair of distinct tetrahedra share a point strictly interior to both. So such a self-intersecting snake might be called a tetrahedral ouroboros.

This example¹ establishes an upperbound of $31$ tetrahedra (adding one more would self-intersect), but clearly this is not the minimum number of tetrahedra. (This example was aiming toward closure, not self-intersection.)

---

         
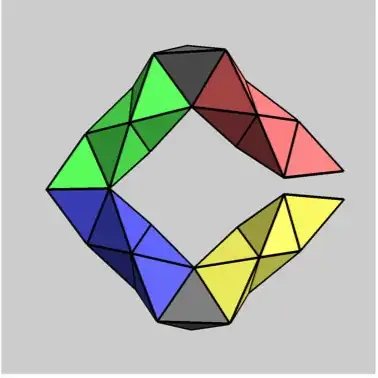
          ^{Fig.6(detail): $QH_7$: $4L+2=30$.}

---

¹ Elgersma, Michael, and Stan Wagon. "The quadrahelix: A nearly perfect loop of tetrahedra." arXiv:1610.00280 (2016).

Answer 1

Michael Elgersma, a coauthor on the paper I cited, provided an answer to my question: an $11$-tetrahedra snake suffices to self-intersect. Here is his illustration of the first $10$ tetrahedra:

---

---

He also sent me a convincing proof of optimality:

Theorem: The shortest tetrahedal snake that has self intersections, has length $11$.