Isbell duality

The (covariant) Yoneda embedding is a covariant functor from a small category ${\displaystyle {\mathcal {A}}}$ into the category of presheaves ${\displaystyle \left[{\mathcal {A}}^{op},{\mathcal {V}}\right]}$ on ${\displaystyle {\mathcal {A}}}$, taking ${\displaystyle X\in {\mathcal {A}}}$ to the contravariant representable functor: [1][8][9]

${\displaystyle Y\;(h^{\bullet }):{\mathcal {A}}\rightarrow \left[{\mathcal {A}}^{op},{\mathcal {V}}\right]}$

${\displaystyle X\mapsto \mathrm {hom} (-,X).}$

and the co-Yoneda embedding[1][10][8][11] (a.k.a. contravariant Yoneda embedding[12][note 1] or the dual Yoneda embedding[17]) is a contravariant functor (a covariant functor from the opposite category) from a small category ${\displaystyle {\mathcal {A}}}$ into the category of co-presheaves ${\displaystyle \left[{\mathcal {A}},{\mathcal {V}}\right]^{op}}$ on ${\displaystyle {\mathcal {A}}}$, taking ${\displaystyle X\in {\mathcal {A}}}$ to the covariant representable functor:

${\displaystyle Z\;({h_{\bullet }}^{op}):{\mathcal {A}}\rightarrow \left[{\mathcal {A}},{\mathcal {V}}\right]^{op}}$

${\displaystyle X\mapsto \mathrm {hom} (X,-).}$

Every functor ${\displaystyle F\colon {\mathcal {A}}^{\mathrm {op} }\to {\mathcal {V}}}$ has an Isbell conjugate[1] ${\displaystyle F^{\ast }\colon {\mathcal {A}}\to {\mathcal {V}}}$, given by

${\displaystyle F^{\ast }(X)=\mathrm {hom} (F,y(X)).}$

In contrast, every functor ${\displaystyle G\colon {\mathcal {A}}\to {\mathcal {V}}}$ has an Isbell conjugate[1] ${\displaystyle G^{\ast }\colon {\mathcal {A}}^{\mathrm {op} }\to {\mathcal {V}}}$ given by

${\displaystyle G^{\ast }(X)=\mathrm {hom} (z(X),G).}$

Origin of symbols ${\displaystyle {\mathcal {O}}}$ and ${\displaystyle \mathrm {Spec} }$: Lawvere (1986, p. 169) says that; "${\displaystyle {\mathcal {O}}}$" assigns to each general space the algebra of functions on it, whereas "${\displaystyle \mathrm {Spec} }$" assigns to each algebra its “spectrum” which is a general space.

note:In order for this commutative diagram to hold, it is required that E is co-complete.[18][19][20][21]

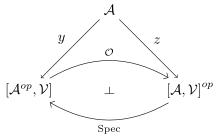
Isbell duality is the relationship between Yoneda embedding and co-Yoneda embedding；

Let ${\displaystyle {\mathcal {V}}}$ be a symmetric monoidal closed category, and let ${\displaystyle {\mathcal {A}}}$ be a small category enriched in ${\displaystyle {\mathcal {V}}}$.

The Isbell duality is an adjunction between the categories; ${\displaystyle \left({\mathcal {O}}\dashv \mathrm {Spec} \right)\colon \left[{\mathcal {A}}^{op},{\mathcal {V}}\right]{\underset {\mathrm {Spec} }{\overset {\mathcal {O}}{\rightleftarrows }}}\left[{\mathcal {A}},{\mathcal {V}}\right]^{op}}$.[3][1][22][23][10][24]

The functors ${\displaystyle {\mathcal {O}}\dashv \mathrm {Spec} }$ of Isbell duality are such that ${\displaystyle {\mathcal {O}}\cong \mathrm {Lan_{Y}Z} }$ and ${\displaystyle \mathrm {Spec} \cong \mathrm {Lan_{Z}Y} }$.[22][25][note 2]