Can an entire star pass through the event horizon of a black hole unharmed?

Question

Can there be any black hole big enough that a regular sized star can pass through its event horizon unharmed?

Answer 1

In order to survive, the star's self-gravitation must be larger than the tidal stretching forces provided by the black hole. If not, then the star will get spaghettified before it crosses the event horizon.

The tidal acceleration on a freely-falling star at the event horizon of a (non-spinning) supermassive black hole is approximately $$g_{\rm tidal}\simeq 2\frac{GM_{\rm BH}r_*}{r_s^3} = \frac{r_*c^6}{(2GM_{\rm BH})^2}\ , $$ where $M_{\rm BH}$ is the mass of the black hole and $r_*$ is the radius of the star. i.e. This is the difference in acceleration between the stellar surface closest to $r=0$ and that furthest away. (A more accurate treatment could integrate over the volume of the star).

Thus the tidal acceleration (i.e. tidal force per unit mass) becomes much smaller at the event horizon of larger black holes. If we demand that this tidal acceleration is less than the star's self-gravity, we can obtain a rough condition for survival. $$ \frac{r_*c^6}{(2GM_{\rm BH})^2} < \frac{GM_*}{r_*^2}$$ $$M_{\rm BH}> \left(\frac{c^6}{4G^3}\right)^{1/2} \left(\frac{r_*^3}{M_*}\right)^{1/2}\ .$$ In terms of solar masses and solar radii: $$ M_{\rm BH}> 1.6\times 10^8 \left(\frac{M_*}{M_\odot}\right)^{-1/2}\left(\frac{r_*}{R_\odot}\right)^{3/2}\ M_\odot\ .$$

Thus a star like the Sun might survive crossing the event horizon of a supermassive black hole of mass greater than 160 million solar masses.

Given that black holes more massive than this do exist at the centres of some active galaxies (for example, the $7\times 10^9 M_\odot$ black hole at the centre of M87), then this seems possible.

Of course, we cannot witness such an event because of gravitational time dilation.

NB: This answer assumes classical GR and in particular does not countenance the idea of a black hole firewall.

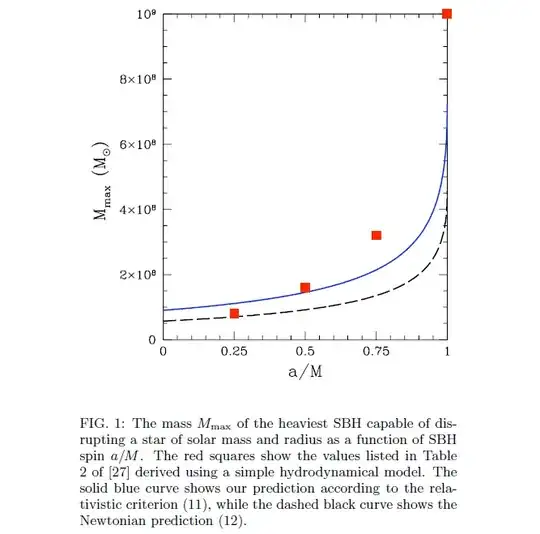
EDIT: The above is all back-of-the-envelope stuff. However, the basic number of 100 million solar masses being some sort of threshold agrees with popular accounts of the stellar spaghettification process. A more detailed theoretical treatment is provided by Kesden (2012), who also considers spinning black holes. The threshold black hole mass becomes larger for a spinning black hole - approximately $7\times 10^{8} M_\odot$ for a maximally spinning black hole - because the event horizon is at a smaller radial coordinate and the tidal forces are commensurately stronger. The picture below shows the dependence of the minimum mass to disrupt a solar-type star prior to crossing the event horizon as a function of the spin parameter of the black hole.

There is also some observational evidence that can be brought to bear on the matter. The spaghettification of a star (or tidal disruption event) can cause a lengthy transient brightening of an active galaxy. Some $\sim 50$ of these events have been obserevd (e.g. Gezari 2021). It turns out that there is indeed a fairly sharp cut-off in the black hole mass distribution for which these tidal disruption events have been seen. This cut-off occurs at $M_{\rm BH} \sim 10^8M_\odot$, suggesting indeed that more massive black holes are able to swallow stars whole.

Answer 2

You can even consider our visible universe to be a black hole. As there are stars around us, they can live quite undisturbed in it. As seen from the part outside the horizon our region is the black hole. Stars from the other side seem to move onto our region but will be seen to end at the horizon (just as we see matter move onto their region, so seen from us it's their region that is a black hole). Then what's the singularity? It's a singularity at the the end of time.
The visible universe has a horizon too. An event horizon, because nothing further away than the horizon can affect us. This can be viewed as the event horizon of the black hole that we are in. There are no tidal effects killing us or the stars. For the stars, the event horizon is not important. And all of them find themselves inside a huge black hole (for which the density can be very small indeed!).

Note that the passage is one way. Once inside the region of the universe just over the horizon, matter can never can go back again.
The same holds for a star or, parts thereof, passing a large black hole. As soon as they have passed the horizon of the hole they are trapped. So if a star has enough velocity so it will not fully be pulled in, it will continue its travel with a lost part (which is, torn of from the star, left behind in the hole. If it is fully eaten then it will never reappear again. Initially, the star can stay as it is (low tidal force), but eventually, it will be torn apart and the particles constituting the star will end up at the singularity.