Considering that the apparent magnitude scale is an inverted scale; what is the lowest apparent magnitude of Saturn that can be seen from Uranus. We are of course talking about when Saturn is viewed from one of the moons of Uranus.
Saturn is in a similar relationship with Uranus as Venus is to Earth. To know this could be helpful when attempting to answer this question.
Leveraging Pierre Paquette's excellent answer and reference to Hilton and Mallama, the magnitude of Saturn can be estimated by:
$$ V = 5 \log_{10} (rd) - 8.95 - 3.7\times10^{-4} \alpha + 6.16\times10^{-4} \alpha^2 $$
Here, $r\approx9.5$ AU is the distance from Saturn to the Sun, $d$ is the distance from Saturn to the observer, and $\alpha$ is the angle of the Sun/Saturn/Observer triangle.
If the observer is located on a planet with orbit inside of Saturn's orbit, it should be clear that the maximum apparent brightness of Saturn should occur when the observer is closest to Saturn, since both $d$ and $\alpha$ are at a minimum.
However, if an observer is on a planet with orbit outside of Saturn's orbit, it certainly isn't the case that Saturn is brightest when closest, since it will be backlit by the Sun from the perspective of the observer.
Using the Law of Cosines, we can compute the distance between the observer and Saturn as a function of $\alpha$:
$$d(\alpha) = r\cos{\alpha}\pm \sqrt{c^2-r^2\sin^2{\alpha}}$$
Here, $c \approx 19.2$ AU is the distance from Uranus to the Sun. This allows us to formulate the expression of magnitude only as a function of $\alpha$.
$$ V(\alpha) = 5 \log_{10} (r^2\cos{\alpha}\pm r\sqrt{c^2-r^2\sin^2{\alpha}}) - 8.95 - 3.7\times10^{-4} \alpha + 6.16\times10^{-4} \alpha^2 $$
Plugging in values from 0 to 180 degrees for alpha, we get the following magnitude phase curve:
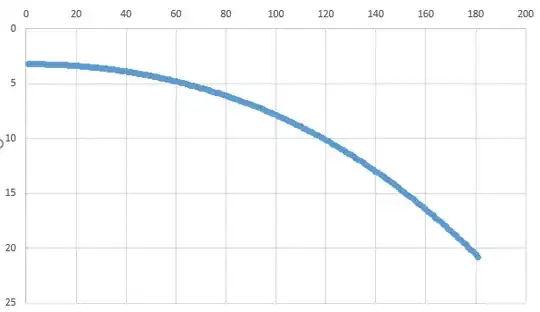
Here the x-axis is $\alpha$ in degrees, and the y-axis is apparent magnitude. It shows that the maximum apparent magnitude of Saturn as seen from Uranus is at opposition (perhaps unintuitively since it is also the maximum distance between the two planets' orbital paths). The value at opposition is about 3.228. As a comparison, Saturn is always much more bright from Earth, varying between -0.55 and 1.17.
Notes:
For convenience, we assume in this answer that the orbits are circular and coplanar. Since both planets have low inclination and eccentricity, we wouldn't expect a very different phase curve from a more sophisticated model.
The above answer is for the apparent magnitude of the sphere of Saturn only. The rings of Saturn can contribute significantly to the brightness of the overall system. Hilton and Mallama provide a more sophisticated equation involving $\beta = \sqrt{\beta_1\beta_2}$, where $\beta_1$ and $\beta_2$ are the inclinations of Saturn's rings with respect to the Sun and the observer respectively. One could get a higher fidelity answer using this equation, perhaps assuming that the maximum ring illumination can occur simultaneously in opposition with $\beta_1=\beta_2 \approx 26.7^\circ$
$$ V = 5 \log_{10} (rd) - 8.914 - 1.825 \sin{\beta}+ 0.026 α - 0.378 \sin{\beta} e^{-2.25\alpha} $$
