I am just beginning to look into this topic, so apologies if there are any striking misconceptions in the following.
From Wikipedia, the Roche lobe is "the region around a star in a binary system within which orbiting material is gravitationally bound to that star". So, to my understanding, this is the region around the star where matter is able to "remain near" the star and not get "sucked away", for example by the other star in the system. Roche lobe overflow seems to be the term used to describe the case where matter falls out of the Roche lobe of one star and hence is "lost" by the star.
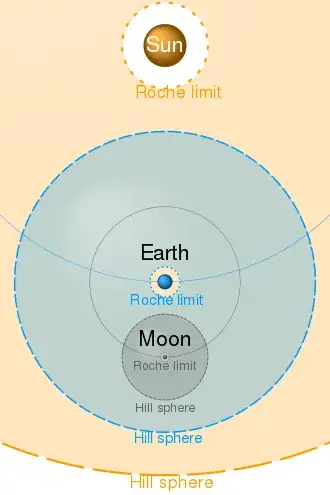
On the other hand, the Roche sphere (or Hill sphere) seems to be a confusingly similar concept! Wikipedia again states, "to be retained by a planet, a moon must have an orbit that lies within the planet's Hill sphere". But isn't this the same as the interpretation of the Roche lobe? The Wikipedia article also mentions stability in the face of perturbations from the gravity of a larger body, but I don't really understand what this means.
Could someone explain in simple terms the difference between the two? Thanks in advance.
(Note: I have seen the question What is the difference between Sphere of Influence and Hill sphere?, but I think that is a distinct question since the SoI is not the same as the Roche lobe; please correct me if I am mistaken!)