2

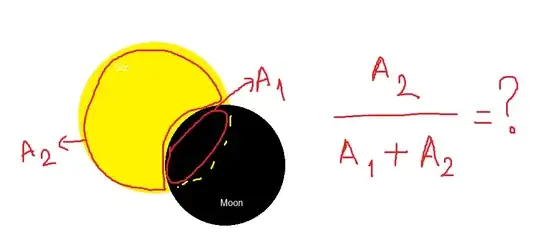
Assume a perfectly spherical Sun and Moon, and ignore atmospheric effects for simplicity. I'm an observer in the origin of my coordinate system, and I know the positions of the centers of the Sun and the Moon. I also know their radii.

At some point during an eclipse, my view of the Moon partially overlaps that of the Sun. Without the eclipse occuring, I could see 100% of the Sun in terms of solid angles. But since the view of Moon now partially blocks the Sun, I can see less. How do I calculate how much of the Sun is still visible to me at that time, as a ratio of solid angles, using the position and radii information?

This is not an observation-based question, since if I was actually observing the event, I could simply shoot a few photos and count the number of pixels and save myself the headache. This is more of a pure geometry question in that sense, to which I haven't found a simple and satisfying answer until now - meaning an (or a set of) equation(s) into which I can plug in the positions and the radii and get the result. To me it looks like that much information is just enough to get the answer, I just can't wrap my head around deriving the maths of it.

enter image description here

arda güler
  • 31
  • 1

1 Answers1

2

From BowlOfRed's Wolfrom link, the area of the asymmetric lense labeled $A_1$ in the O.P's post is $$A_1 = r^2\cos^{-1}\bigg(\frac{d^2+r^2-R^2}{2dr}\bigg) +R^2\cos^{-1}\bigg(\frac{d^2+R^2-r^2}{2dR}\bigg)- \frac{1}{2}\sqrt{(-d+r+R)(d+r-R)(d-r+R)(d+r+R)}$$

Here, $d$ is the distance between the Sun center and Moon center, $R$ is the apparent radius of the Sun, and $r$ is the apparent radius of the Moon.

Then the visible area of the Sun is simply:

$A_2 = \pi R^2-A_1 $

I suspect it's not possible to calculate this simply as a ratio of solid angles.

Connor Garcia
  • 16,240
  • 4
  • 43
  • 96
  • 3
    It might be worht including that $r\approx R$ , and this approximation simplifies the formulae somewhat. – James K Jun 05 '23 at 21:04