NOTE: At the end of my post the output is shown as a list of tuples. The first value in each tuple is the result and the second value is the estimated error on that result. Near the end, the estimated error is of order one part per thousand of the result, which is much too high for a numerical integration over such smoothly varying functions.
1. Inverse Compton radiation of electron collectives
$$j(\nu)=\int P(\nu)N(\gamma)\mathrm{d}\gamma=8\pi r_0^2chG$$ thereinto
$$G=\int_{\nu_1}^{\nu_2}\int_{\gamma_1=\frac12(\frac{\nu}{\nu_i})^{1/2}}^{\gamma_2} N(\gamma)f(\frac{\nu}{4\gamma^2\nu_i})n_{\mathrm{ph}}(\nu_i)\mathrm{d}\nu_i\mathrm{ d}\gamma $$ thereinto $$f(x)=2x^2\mathrm{ln}x+x+x^2-2x^3,0<x<1$$ where $x = \nu/4\gamma^{2}\nu_{i}$
2. Background photon number density distribution in a radiated field
$$n_{\mathrm{ph}}(\nu_i)=\frac{8\pi\nu_i^2}{c^3}\frac1{e^{\frac{h\nu_i}{kT}}-1}$$
3. Electrons have a power-law distribution
$$N(\gamma) = N\gamma^{-n}$$
N0 = 1
h = 6.626e-27 # Planck const in erg. s
c = 3e10 # Speed of light in cm/s
k = 1.38e-16 # Boltzmann constant in erg/K
r0 = 2.82e-13 # Classical electron radius in cm
## integating gamma--> nu_i ,nu is parameter
def integrand_G(gamma,nu_i,nu):
N_e = N0 * gamma(-3)
N_ph = 8 * np.pi * nu_i2 / (c*3 (np.exp(hnu_i/(kT_ph))-1) )
x = nu / (4 * gamma**2 * nu_i)
const = 8 * np.pi * r0**2 * c * h
if 0 < x < 1:
fx = 2 * x**2 * np.log(x) + x + x**2 - 2*x**3
result = const * fx * N_e * N_ph
return result
else:
return 0
def range_gamma(nu_i,nu):
return [0.5* (nu / nu_i)**0.5,np.inf]
range_nui = [1e13,1e16]
def j_nu(nu):
integrand, err = nquad(integrand_G,[range_gamma,range_nui],args=(nu,))
return integrand,err
T_ph =5e4
nu01 = np.logspace(13,16,50)
gamma1 = 10
nu_values =4/3gamma12 nu01
j_nu_values = [j_nu(nu) for nu in nu_values]
j_nu_values
the result is
[(4.646891358736883e-25, 9.732928577801494e-34),
(4.0358780167911975e-25, 3.7331558505127706e-34),
(3.50520595581472e-25, 8.745269160624114e-37),
(3.044311236175784e-25, 4.596524332722152e-34),
(2.6440189335175633e-25, 6.9773996637028405e-37),
(2.2963605183798276e-25, 2.32847015875059e-34),
(1.9944152312040706e-25, 5.106011672520151e-35),
(1.7321723128286085e-25, 6.167458221137299e-35),
(1.5044113565389222e-25, 6.549329044601913e-35),
(1.3065983749075148e-25, 6.1367624503818e-35),
(1.1347955500240598e-25, 5.196262110593544e-35),
(9.855828423034596e-26, 4.672407189709615e-35),
(8.559899083742284e-26, 4.015760139155061e-35),
(7.434369712819832e-26, 3.4425082332554275e-35),
(6.456834652685337e-26, 2.957012268335199e-35),
(5.607834334707997e-26, 2.5772446384380916e-35),
(4.8704679021211965e-26, 2.3382198801399686e-35),
(4.230056768532779e-26, 2.2967597901824962e-35),
(3.6738524146513086e-26, 2.540934279247937e-35),
(3.1907826064254274e-26, 3.2026146513980704e-35),
(2.7712309826214774e-26, 4.4521946638201733e-35),
(2.4068456241343245e-26, 6.432951098088548e-35),
(2.0903728116056675e-26, 1.0795160235615729e-35),
(1.8155125637870292e-26, 3.831168995920699e-36),
(1.5767933111091125e-26, 2.6129469178833845e-36),
...
(8.166934445646721e-28, 1.7567146260202947e-33),
(7.0930754638972155e-28, 2.1515340634505886e-33),
(6.160414678071309e-28, 6.411250698120658e-34),
(5.350517710760285e-28, 2.308277273356424e-31),
(4.647002306856651e-28, 2.4616285151340818e-31)]
```
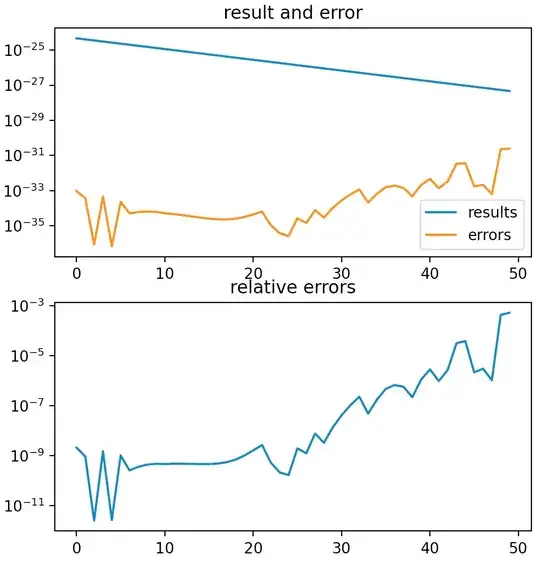
My source code is attached to the issue
– Shayu xiao Jan 04 '24 at 01:39