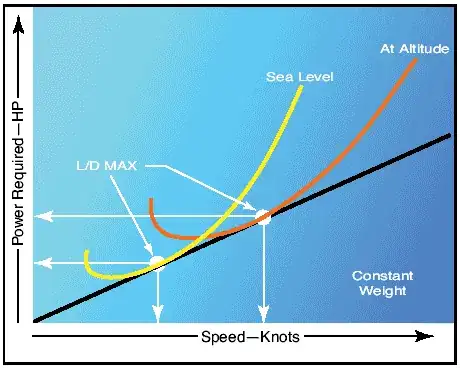
Chapter 11 of the PHAK states, "If a change in altitude causes identical changes in speed and power required, the proportion of speed to power required would be unchanged. The fact implies that the specific range of a propeller driver aircraft would be unaffected by altitude. Actually, this is true to the extent that specific fuel consumption and propeller efficiency are the principal factors that could cause a variation of specific range with altitude. If compressibility effects are negligible, any variation of specific range with altitude is strictly a function of engine/propeller performance. An aircraft equipped with a reciprocating engine experiences very little, if any, variation of specific range up to its absolute altitude."
I looked at the POH's of both a Cessna 172 S model, and a Piper Warrior, and it seems as though both airplanes experience a significant increase in range with higher cruising altitudes. Can anyone explain this?