1

in this excellent answer, it states this :

A well-known effect of wing sweep is the variation of induced downwash along the span from the trailing wake that produces an additional lift distribution characterized by increased loading on the aft wing and reduced additional lift on the forward wing. For a wing with no twist or bend, this results in a significant rolling moment, tending to roll the forward wing downward. There is also a yawing moment from the asymmetrical distribution of induced drag that tends to unsweep the wing.

My question is, what makes the induced downwash along the span vary? Also, when it says "trailing wake", does that mean the wake turbulence from the aircraft, and if so how would that interfere with the induced downwash? (the 2 big vortices formed by the aircraft is what I mean by wake turbulence)

Wyatt
  • 1,943
  • 1
  • 9
  • 24
  • A bit unrelated, but I was thinking about this also, so I’ll put it here. Say your left wing for whatever reason has no tip vortex. I always thought that would make you roll to the right, as the downwash from the vortices would be “pulling” the right wing down. Is that correct? – Wyatt Mar 23 '24 at 02:55
  • 1
    Good question. Wouldn't the absence of the tip vortex indicate the left wing was producing no lift? As indicated by the downwash, isn't the net displacement of momentum downward on the right wing? In that case, with lift indicated on the right wing, wouldn't the aircraft roll to the left? – Thomas Perry Mar 23 '24 at 03:41
  • Yes that would definitely indicate that, but pretend that the lift is still being created but somehow the tip vortex isn’t. Isn’t possible in real life, but just a thought experiment. – Wyatt Mar 23 '24 at 04:19
  • @ThomasPerry Also, did you mean downwash from the tip vortices (induced downwash) or just the plain downwash from the wing? – Wyatt Mar 23 '24 at 04:56
  • Conceptually, downwash and the presence of tip vortices are all part of one continuous process. – Thomas Perry Mar 24 '24 at 03:13
  • Related: https://aviation.stackexchange.com/questions/104365/what-happens-to-tip-vortices-in-a-sideslip? -- see all answers – quiet flyer Mar 25 '24 at 12:49

1 Answers1

4

This effect is really only substantial for swept wings.

Here is the lift distribution on an un-swept rectangular wing at 10deg AoA at 0 and 10 deg Beta.

enter image description here

Notice the general slight reduction in lift - but also the slight asymmetry introduced.

If you were to plot the wakes, they are pretty uninteresting. The 10deg Beta wake is essentially sheared 10deg to mostly align with the freestream.

However, let's look at the same wing with 20deg of sweep. If you draw some velocity diagrams, you'll find that the left and right wing seem to end up seeing substantially different angle of attack.

enter image description here

It is clear that the two half-wings are seeing very different flow situations. This results in a dramatically changed lift distribution for the two.

enter image description here

Notice the large change in lift distribution on the two wing halves. It is as if the right wing sees a higher angle of attack than the left wing.

The wake is the sheet of vorticity that trails behind a lifting surface. It is stronger at the wingtips than across the rest of the wing, but it exists everywhere there is circulation.

Edits:

It looks like I opened a can of worms with the angle of attack analogy.

I based my comment on foggy memories of a classical argument for a $C_{l,\Beta}$ derivative (dihedral effect, rolling moment wrt. sideslip) and how it depends on wing sweep angle.

For example, from: Etkin B. and Reid, L.D., "Dynamics of Flight; Stability and Control", Third Edition. John Wiley & Sons 1996.

enter image description here

quiet flyer -- My memory was wrong -- they make an argument based on velocity magnitude perpendicular to the wing -- not based on velocity triangles changing the local angle of attack. I think this tracks better with your understanding.

Interestingly, the dihedral effect due to dihedral is calculated with the velocity triangles I remember.

Amusingly, he goes on to make an argument about the oblique wing in this discussion...

enter image description here

Sophit - you're right, I read the OP's question without clicking on the link. So I was answering for actual swept wings.

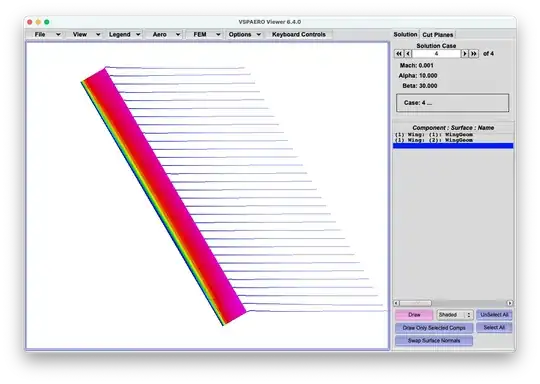
For Robert DiGiovanni, Here is a set of load distributions for the straight wing at 0,30 deg Beta and 5,10 Alpha.

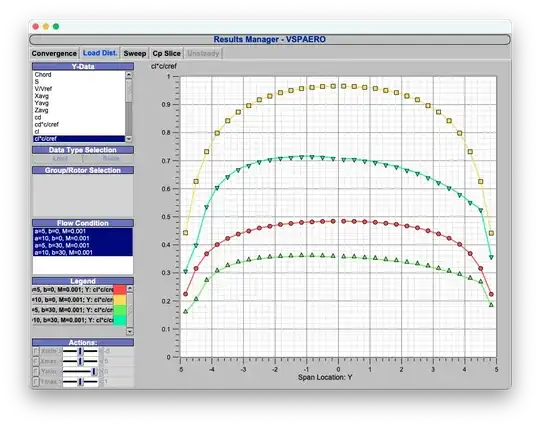
enter image description here

And the 30deg Beta, 10deg Alpha plot of delta Cp and the wake -- rotated about 30 degrees to make it look like an oblique wing.

enter image description here

Rob McDonald
  • 10,966
  • 1
  • 13
  • 34
  • Not sure if I’m not picking up on something, but is the reason the 2 half’s of the wings end up at different AoA because of the tip vortices? – Wyatt Mar 23 '24 at 05:11
  • Please note that in the linked answer, with "swept wing" they actually mean "oblique" wing... The present answer, albeit being technically perfect, is therefore formally wrong. – sophit Mar 23 '24 at 06:37
  • @RobMcDonald please run the unswept wing at 30 degrees beta and also try 5 degrees AoA (to continue work on oblique wings). The swept case reveals that a yaw unsweeps one and sweeps the other more (good for Dutch Roll studies). I am curious to see if the effect of sweep on lift is linear, especially at higher beta. – Robert DiGiovanni Mar 23 '24 at 07:20
  • Seperate question: in the view from above of the swept wing, if the airflow is crossing from right to left in the aircraft's reference frame, why do the airflow lines right at each wingtip seemed to be kinked the opposite way? I.e. on the right wingtip the line bends slightly outboard but on the left wingtip it bends slightly inboard? Is that because the right wing is generating more lift than the left wing? – quiet flyer Mar 23 '24 at 14:52
  • I'll accept "go to chat" at the first opportunity and delete most of these comments. What it really all boils down to is this-- we know that sweeping a wing tends to reduce its max Cl and generally flattens out the Cl vs aoa curve. (There's a figure showing this in the book Aerodynamics for Naval Aviators.) In the sideslip case, one wing is much more swept than the other, relative to the airflow. So it's no surprise that it's lift coefficient is reduced. Is the reduction in lift coefficient due to sweep specifically attributable to greater induced downwash? – quiet flyer Mar 23 '24 at 16:09
  • Food for thought-- this related answer https://aviation.stackexchange.com/a/9292/34686 does state that sweep causes the "effective angle of attack" to vary between the two wings in a sideslip. I guess "effective angle of attack" is measured with one edge the protractor normal to the quarter-chord line? I'll have to think about that a bit. I'm not sure it's really fair to list points 1 and 2 at the front of that other answer as 2 different phenomena, aren't they 2 different ways of stating the same thing? – quiet flyer Mar 25 '24 at 12:36
  • (Ctd) Anyway in that answer by "effective a-o-a" it's pretty clear he's defining a-o-a relative to the free-stream flow, i.e. not considering induced downwash. The answer doesn't seem to consider induced downwash, or differences in induced downwash between the two wings, at all. And yet he still comes to the conclusion that sweep tends to produce a roll torque during sideslip (at least at non-zero a-o-a). – quiet flyer Mar 25 '24 at 12:42
  • (Ctd) No surprise there, but I guess I'm circling back to my question of whether the lift difference between the two (swept) wings highlighted in your answer can really be attributed primarily or largely to differences in induced downwash and other effects related to displacement of the tip vortex/ wake vortex systems, or not. – quiet flyer Mar 25 '24 at 12:43
  • 1
    I would agree that points 1 and 2 in the other post are not different phenemona. When you take the simple sweep theory approach of 'normal velocity matters', you can book-keep the change as a change in chord, velocity, alpha, or whatever. If the whole expression is multiplied by $\cos(\Lambda)$, then you can choose to interpret that effect on any single term. I would argue that this is a fundamental geometric effect -- it is not an effect of induced downwash. – Rob McDonald Mar 25 '24 at 16:13