11

I'm trying to figure out the lift coefficient of an A320.

What I'm doing is the following: during cruise, the lift is equal to the weight of the aircraft ($mg$) so that I used the cruise table taken from the FCOM to get the speed, the wing area is known ($122.6 m^2$) and I calculated using a tool online the air density at FL290 (29,000 ft).

The result is that the lift coefficient is $0.03029$. Is it right for the assumptions given above?

Next, if I want to relate the $C_L$ with the Angle of Attack, what is the formula and the procedure?

Danny Beckett
  • 16,627
  • 28
  • 98
  • 176
Afe
  • 1,501
  • 1
  • 12
  • 21
  • 2
    Well.... I doubt that any current airliner will be able to fly with just 0.03 of $C_L$, did you mulitplied the mass by the gravity? – Trebia Project. May 04 '15 at 10:11
  • 50000kg is the "weight" so already multiplied by g, that's not the mass. – Afe May 04 '15 at 11:46
  • Well, first hint for knowing that the gravity shall be used is that "weight" is measured in Kg instead of N. Second is having a so low $C_L$, having actually lower $C_L$ than usual "C_D$ values. Another warning message is that if 50000 is actual "weight" the mass will be 5000Kg, which means that for an A320 being an airplane of more than 100 passenguers of around 75Kg (in mass) having a total mass of 7500Kg we have a negative mass of the structure of -2500Kg for reaching the the 50000/9,8 mass value. In that sense, I think it is more likely that "weight" is actually "mass" than other option – Trebia Project. May 04 '15 at 13:03
  • It's the same as when I say for example: "My weight is 60Kg". This means that my mass is 60/9.8. – Afe May 04 '15 at 15:34
  • My point is that, although it is said "weight" it actually means "mass". Having a $C_L$ of ust 0.03 is unphysical. An airplane of 100 passenguers with a actualy weight of 50kN is not possible .... – Trebia Project. May 04 '15 at 15:37
  • The Operating Empty Weight for an A320 is 42600Kg as it's possible to see here: http://en.wikipedia.org/wiki/Airbus_A320_family#Specifications – Afe May 04 '15 at 15:44
  • That's the point, although says Operating Empty Weight is actually Operating Empty Mass – Trebia Project. May 04 '15 at 16:04

1 Answers1

9

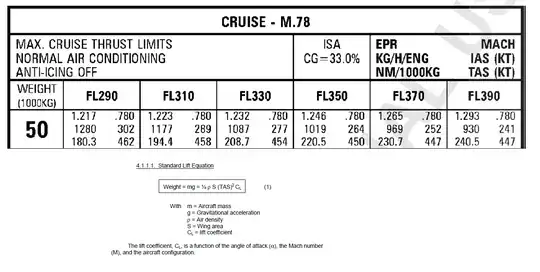
I found a different number for $C_L$, please check your calculation:

$C_L=\frac{2 m g}{\rho V^2 S}$

substitute: $ m = 50000 \textrm{ kg}\\ g = 9.81 \textrm{ m}/\textrm{s}^2\\ V = 462 \textrm{ KTAS} = 237.67\textrm{ m/s}\\ S = 122.6 \textrm{ m}^2\\ \rho = 0.475 \textrm{ kg}/\textrm{m}^3 $

This will give: $C_L = 0.298$

Note that this lift coefficient is for the total aircraft. It includes the lift of the wing, the fuselage lift and also the negative lift of the vertical stabilizer. There is also a small vertical component of thrust that is neglected.

Now that we have an estimate of the lift coefficient, we can estimate the angle of attack. Normally the lift coefficient is assumed to vary linearly with the angle of attack:

$C_L = \frac{\textrm{d}C_L}{\textrm{d}\alpha}\cdot (\alpha-\alpha_0)$

$\alpha_0$ is the zero-lift angle of attack, the angle of attack at which the wing does not generate any lift. For symmetric airfoils, $\alpha_0 = 0$, for chambered airfoils $\alpha_0 < 0$.

I don't know what that angle is for the A320, it will be difficult to obtain. Let's assume for now it is -1.2 degrees.

For infinite long wings in incompressible flow the lift slope $\frac{\textrm{d}C_L}{\textrm{d}\alpha}$ is $2\pi$.

$(\alpha-\alpha_0) = \frac{C_L}{2\pi} =0.0474 \textrm{ rad} \approx 2.72^\circ$

This would result in an angle of attack of $\alpha \approx 1.52^\circ$

Because the wing of the Airbus A320 is not infinitely long but has a span of about 30 meters (excluding the fuselage) we need to correct for that. The reason we need to correct for the finiteness of the wing is that the circulation will cause the local angle of attack of the wing to be lower than the free stream angle of attack. The effective angle of attack $\alpha_{eff} = \alpha - \alpha _i$

The induced angle of attack $\alpha_i$ is given by:

$\alpha_i = \frac{C_L}{\pi AR} = \frac{C_LS}{\pi b^2}$

substitute: $ S = 122.6 \textrm{ m}^2\\b = 30 \textrm{ m} $

gives $\alpha_i = 0.0129 \textrm{ rad} \approx 0.74^\circ$

Adding this to our earlier angle of attack results in:

$ 1.52 + 0.74 = 2.26^\circ$

This may not be very accurate as

a) the zero-lift angle of attack may be very different,

b) the lift slope may be flatter due to compressibility effects

Federico
  • 32,559
  • 17
  • 136
  • 184
DeltaLima
  • 83,202
  • 11
  • 272
  • 366
  • The two densities used are slightly different. I think this could explain the 1.6% difference. – Thunderstrike May 04 '15 at 08:42
  • @MikeFoxtrot the difference is almost 90%, or 883% depending on which CL you take as denominator... – DeltaLima May 04 '15 at 09:00
  • took the liberty of fixing a comma-decimal dot typo – Federico May 04 '15 at 11:08
  • @Federico thnx! – DeltaLima May 04 '15 at 11:08
  • @DeltaLima Just spotted the decimal points was off so indeed :P The online tool gives a density of 0.47545 as compared to 0.475 that you use. – Thunderstrike May 04 '15 at 11:19
  • @DeltaLima $\alpha_0 < 0$ ??? How did you estimate 0 lift angle? – Trebia Project. May 04 '15 at 15:01
  • @DeltaLima notice as well that $2\pi$ is the ideal slope without compressibility effects and as well, referred to the "ideal" surface. I think is a good estimation, but if somebody reads this and wants to perform a more detailed estimation double check the definition of surface area. Is winglet included? Is the are within the fuselage connecting both side of the wing included? That might change the number (is not a simple question...) – Trebia Project. May 04 '15 at 15:06
  • @TrebiaProject. I don't understand your first remark, did you expect $\alpha_0 > 0$ ? $2\pi$ is the slope for the infinite wing which has no winglets nor a fuselage. There are so many way – DeltaLima May 04 '15 at 16:01
  • @DeltaLima arg... forget my comment about "\alpha_0" I made a mistake confusing "\alpha_0" and the alpha of minimum drag. For wing efficiency normal actual values are around 3-4. My question as well is how you estimate the value "\alpha_0" – Trebia Project. May 04 '15 at 16:17
  • @TrebiaProject. The value $\alpha_0$ was an educated guess. What "normal actual values" are you referring to? Do you mean the $alpha$ during cruise flight is usually in the 3 - 4$^\circ$ range? Note the OEM is 42,600 kg and the MTOM is 78,000 kg, so the aircraft in this question is very light at 50,000kg. That could explain the lowish angle of attack. – DeltaLima May 04 '15 at 19:29
  • @DeltaLima I mean the wing efficiency or wing slope is aroudn 3-4 instead of 6.28. Yep, looks like unloaded airplane. – Trebia Project. May 04 '15 at 20:12
  • @TrebiaProject. Ah, I see. Effectively the lift slope is 4.94 in my calculation. Because $\frac{\textrm{d}C_L}{\textrm{d}\alpha_{eff}} = 2\pi$ and $\frac{\textrm{d}\alpha_{eff}}{\textrm{d}\alpha} = \frac{b^2}{b^2\cdot2S}$. – DeltaLima May 04 '15 at 20:43
  • According to A320 FCOM the span (b)=34.6 m not 30m is there any difference in dimensions? – Mike Golf Mar 14 '18 at 09:45
  • @MikeGolf The difference is approx. 4 meters of fuselage diameter. – DeltaLima Mar 14 '18 at 15:43