Is gravity less on an airliner at cruise altitude?

Question

Is the force of gravity less on an airliner at cruise speed and altitude? I'm not talking about a special reduced gravity flight with a parabolic flight path, just a typical long distance flight.

Seems to me there should be less as passengers are further away from the centre of the earth, and also possibly a tiny effect from the speed the plane as it travels round the curve of the earth (altitude remaining constant) but does anybody actually know how much less?

Answer 1

There is less gravitational force, but by how much? An insignificant amount. The gravitational force of attraction between two objects is given by,

$\displaystyle F_{\mathrm g} = \frac{G m_{1} m_{2}}{R^2}$,

where,

$G$ is the graviational constant,

$R$ is the distance between the object's centers, and

$m_{1}$ and $m_{2}$ are the masses of the objects.

Instead of finding the variation in force between the aircraft and earth, it would be be better to find the variation in the acceleration due to gravity, $g$ (as $F_{\mathrm g} = m_{\mathrm a} g$, with $m_{\mathrm a}$ being the mass of the airliner)

We have, on earth's surface,

$\displaystyle g = \frac{G m_{\mathrm e}}{R_{\mathrm e}^2}$

where,

$m_{\mathrm e}$ is the mass of the earth, and

$R_{\mathrm e}$ is the radius of the earth.

For the aircraft at an altitude $h$ above the surface of the earth, this becomes,

$\displaystyle g_{h} = \frac{G m_{\mathrm e}}{\left(R_{\mathrm e} + h\right)^2}$

Taking ratio, we get,

$\displaystyle \frac{g_{h}}{g} = \left(1 + \frac{h}{R_{e}}\right)^{-2}$

Plugging in numbers, we get, for an airliner cruising at 12 km,

$g_{h} = 9.773\ \mathrm{m\ s^{-2}}$,

or about 0.37 % less compared to the sea level value. This is quite small and would not be noticable to all but the sensitive instruments.

Answer 2

Gravity itself

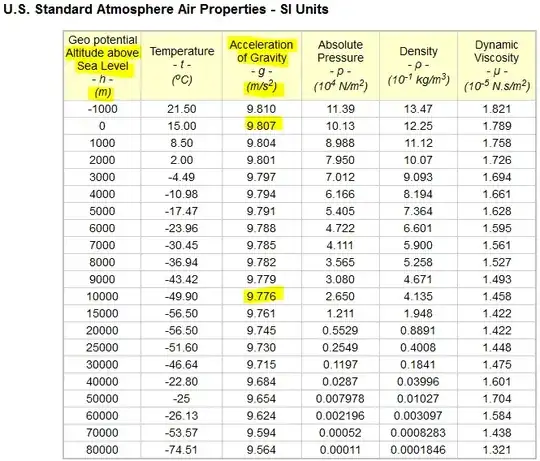
@aeronalias is absolutely right. Given the gravitational acceleration of $g=9.81m/s^2$ on the ground, a perfect spherical earth of radius $R_E=6370km$ with homogenous (at least: radially symmetric) density, one can calculate the gravitational acceleration at an altitude of $h=12km$ by

$$g(h)=g\cdot\frac{R_E^2}{(h+R_E)^2}= 9.773 \rm{m}/s^2$$

Expressed in terms of $g$, the difference is

$$g_\rm{diff} = 0.0368565736 m/s^2 = 0.003757g$$

Centrifugal forces

The question also asks for the centrifugal effect on the aircraft as it travels round the curve of the earth, which has not yet been answered yet. The effect is considered small, but compared to the effect on gravity itself, it isn't always.

I got some heavy objections on my answer and I have to admit, I really don't see their point. Therefore, I've edited this section and hope this helps.

In general, an object moving on a circular path experiences a centrifugal acceleration, pointing away from the center of the circle:

$$a_c=\omega^2r=\frac{v^2}{r}$$

$\omega=\frac{\alpha}{t}$ is the angular speed, i.e. the angle $\alpha$ (in radians) the object travels in a given time $t$ (in seconds).

Now let's consider a "perfect" Earth as described above, plus no wind. A balloon hovering stationary over a point at the equator at 12km altitude will do one revolution ($\alpha=2\pi[=360°]$) in 24 hours. So it is $\omega=\frac{2\pi}{24\cdot60\cdot60s}$. Together with $r=R_e+h$, one gets for the balloon:

$$a_{cb}=0.03374061 m/s² = 0.0034394098 g$$

The circumference of the circle the balloon flies is $2\pi(R_e+h)=40099km$

Now consider an aircraft flying east along the equator at the same altitude at 250m/s (900km/h, 485kt) with respect to the surrounding air. (Keep in mind: no wind). In 24h, this aircraft travels a distance of 21600km, or 0.539 of the circumference. This means the aircraft does 1.539 revolutions of the circle in 24h, which means its angular speed is $\omega=1.539\cdot\frac{2\pi}{24\cdot60\cdot60s}$. Thus, the centrifugal force on the aircraft flying east is

$$a_\rm{ce} = 0.0799053814 m/s^2 = 0.0081452988 g$$

The same way, one can calculate what happens when the aircraft flies west: $\omega=(1-0.539)\cdot\frac{2\pi}{24\cdot60\cdot60s}$

$$a_\rm{cw} = 0.0071833292 m/s^2 = 0.0007322456 g$$

Comparison

Let's write the values together to compare them. I've also added how much lighter a 100kg (220lb) person would feel due to the effects:

                                             | "weight loss"
g_diff = 0.0368565736 m/s²  = 0.003757 g     | 376gram (0.829lb)
a_cb   = 0.03374061   m/s²  = 0.0034394098 g | 344gram (0.758lb)
a_ce   = 0.0799053814 m/s²  = 0.0081452988 g | 815gram (1.797lb)
a_cw   = 0.0071833292 m/s²  = 0.0007322456 g |  73gram (0.161lb)

Note: The 100kg is what a scale at the North Pole (i.e. without any centrifugal effect) shows. The person already feels 344g lighter on the ground at the equator. The balloon doesn't change this (much). But moving east/west has a larger effect on the weight than gravity alone. A person flying west feels even heavier than on ground!

Maybe another table, showing the weight of the person:

                                             kg      lb
1. Man at north pole                       100.00  220.46
2. Man at equator                           99.66  219.70
3. Man at equator, in balloon               99.28  218.88
4. Man at equator, in aircraft flying east  98.81  217.84
5. Man at equator, in aircraft flying west  99.55  219.47 <- More than 3.

The numbers shown are only valid at the equator and for flights east / west. In other cases, it becomes a little more complex.

---

EDIT: Being curious on how this depends on latitude, I created this plot about the absolute acceleration an aircraft experiences.

The radius in the equation of the centrifugal force is the distance of the aircraft to the axis of the Earth. It is clear that it decreases when moving away from the equator, and so does the acceleration.

The speed of the aircraft flying west will cancel out the speed of the earth at about 57° N / S, i.e. there is no centrifugal force. At larger latitude, the aircraft will fly in the opposite direction around the axis of the earth, building up a centrifugal force again.
Near the poles, both aircraft become centrifuges (theoretically). E.g. flying a circle of 500m radius gives an acceleration of 12.7g. This is why the data rises to infinity there.

(When doing the math, one has to keep in mind that gravity always points to the center of the earth, while the centrifugal force points away from the axis. You can't just add them)

Answer 3

You are correct that the force of gravity is slightly less the further you get from the earth. Airlines typically cruise around 30,000 - 35,000 feet. We can use as a proxy measurement the force of gravity on Mt. Everest, which is 29,000 ft.

The force of gravity on Everest is about 0.434% less than the standard 9.8N/kg. This means that one pound at Sea Level would weigh about 0.995 lbs. at 29,000 ft. Or, a typical 180 lb. human would weigh 179.1 lbs.

I don't consider the speed of the aircraft going around the earth to be significant. Any centripetal force would be extremely tiny.

Answer 4

Here's the Fermi Estimate version, in case the math in Aeroalias's answer is difficult to follow:

It's been said that the ISS experiences 0.9 G (90% of standard gravity at sea level), which is of course canceled out by their orbital velocity so the astronauts inside feel like they're in 0G.

Airplanes are said to fly a mile high, and the ISS is over 100 miles high--these are not particularly accurate numbers, but they're good enough for order-of-magnitude estimations.

Therefore, without any complicated math, we would expect an airplane to experience 99.9% of standard gravity. As Aeroalias's answer works out to 99.63%, this is a pretty good estimate.

Answer 5

Gravity decreases with altitude

See this table providing gravity at different altitudes:

^{Gravity field at different altitudes (source: The Engineering Toolbox)}

At a height of 10 km, gravity is 9.776 against 9.807 at sea level. That's a variation of 0.32%, which I consider as significant from an aircraft design angle, as it allows to reduce the fuel consumption in a larger proportion.

Can we sense the gravity difference at the altitude of 10 km?

Such difference cannot be sensed by a human, a metering instrument is required. Sensing 0.3% difference just requires a scale. If you "weight" a mass of 100 kg, then at a height of 10 km, the scale will just display 99.7 kg.

Note: A gravity value of 9.78 m/s² already exists on Earth, e.g. in Mexico city and in Singapore, due to gravity anomalies.

How fast gravity decreases?

The center of the gravity field is near the center of the Earth. The surface of the Earth is at 6,400 km from the center and the value of gravity is 9.81 m/s² or g.

Each time the distance from the center doubles, the gravity value is divided by 4: At 12,800 km, the value is 1/4 g. This progression is said to be an inverse square law, which looks like this:

^{Curve of an inverse square law (source)}

Many physical quantities are based on this same law (light intensity, sound intensity, radio signal intensity). As you can see after 3 or 4 Earth radius, the variation has slowed down a lot, but it continue to decrease and will never reach zero. it means any object in the universe has an impact on all other objects! (but a small one).

The gravity value decreases when climbing, but also decreases when going underground. Near the center of the Earth the gravity is null (at least that's what we believe, we are not going to be able to check until a very long time, it's easier to explore space than the depths of our planet). This is the complete picture of the gravity:

^{Gravity field according to the preliminary reference Earth model}

Gravity is a puzzling force not yet understood. We know local effects of the gravity, but we ignore the reasons of such effects.

Answer 6

Most of questions deal with the gravity reduction due increased distance to the Earth but there is also centrifugal force caused by movement. This force allows spaceships to circle the Earth with no power applied and causes weightlessness inside - just increased distance would not be enough for these effects. An airplane is also flying around the Earth, same as a satellite does, just much slower.

This effect described here and may reduce the perceived weight (the aircraft feels lighter and everything inside is lighter) but can also increase it (depending on how the flight direction is related to the rotation of the Earth). The effect is somewhat about 0.3 % of mass at the speeds close to the speed of sound so comparable to the effect from the increased altitude.

Answer 7

Most answers here are from a perspective of "at a height of X, you weigh Y". Lets turn this around.

At the altitude of the ISS, gravity is about 10% less. I doubt you'd notice 10% reduction in weight (double-blind, if such a thing were possible), without using measuring equipment. That's 400km up (250 miles), and well outside our atmosphere.

The only reason people are "weightless" on the ISS, is that they are in orbit.

Things in orbit are always weightless. The scales you are standing on is falling at the same speed you are. This can happen at any altitude - if you kick a ball, it is in orbit - an orbit that intersects with the surface of the earth, so it can't complete the orbit.