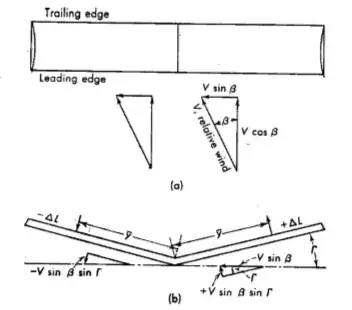
The explanation lies in the fact that a rolled wing creates a oblique relative wind, and that a wing with a dihedral angle seen from an oblique direction is having a larger angle of attack on the side in this direction:

Because of the dihedral angle, for the wind coming from an oblique direction on the right of the aircraft, the right wing shows a larger AoA. This is even more important for a larger dihedral angle.
Visual demonstration
On the image below:
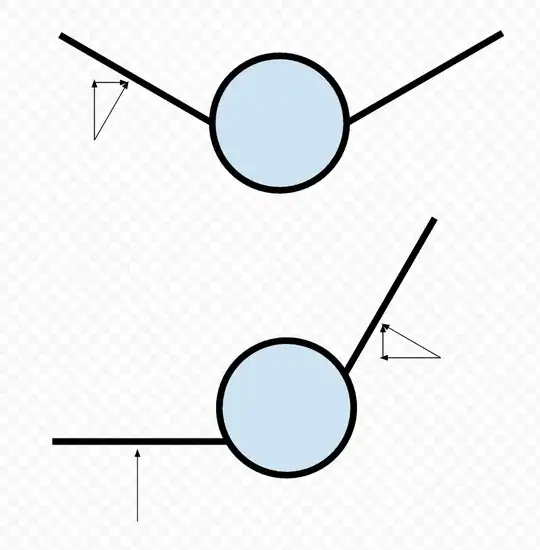
On the left side, there is an aircraft which is horizontal, flying level, and in a relative headwind. Obviously the action of the wind will be the same on both wings, whatever the dihedral angle, and the lift vector is oriented vertically (in blue).
On the right side, the aircraft has been disturbed and for some reason is now rolled to the right without pilot action. Imagine the heading is still the same.

The key to see what will happen is to understand the right wing now develops more lift than the left wing, the difference being proportional to the dihedral angle. As soon as this is clear, we can anticipate the roll angle will be cancelled automatically, without pilot action.
Let's look at the rolled aircraft:
The lift vector, which is still normal to the wing, is no more vertical. From a mathematical point of view it can be split into two components along arbitrary directions. If we choose a resolution along the vertical and horizontal axes, we see the vertical component is now smaller (therefore the aircraft starts descending) and a horizontal component appeared in the process.
The horizontal component pulls the aircraft to the right side. As the heading is unchanged, the aircraft is not in a turn, and no centrifugal force opposes this horizontal component of the lift, therefore the aircraft starts side-slipping and the relative wind is no more a headwind, there is some crosswind from the right side.
Angle of attack seen from the relative wind standpoint:
When the aircraft was flying in a headwind, the angle of attack was the same for both wings.
With the crosswind component, the angle of attack of the right wing is higher than the angle of attack of the left wing. The difference is small when the dihedral angle is small, and increases with its value. To make this apparent, I added wings with higher dihedral angles to the aircraft:

Note: The difference appears only when the wind is off axis. This means the dihedral effect on the angle of attack exists only when there is a sideslip.
Of course because the angle of attack is larger on the right, a recovery moment starts developing and counteracts the initial roll. The aircraft returns to the horizontal after some damped oscillations around the longitudinal axis.
The lateral stability is of prime importance for general and commercial aviation aircraft. The dihedral angle is the most simple mean to obtain this stability, there are others.
Stability from swept wing, due to spanwise flow
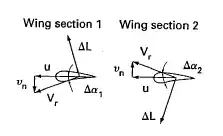
Lift is generated taking into account the airflow parallel to the chord which is accelerated. Air moved in a perpendicular direction is not accelerated and doesn't create any lift, see left image:

(By principle, a swept wing decreases the amount of lift created, this is compensated by other benefits that make it useful anyway).
If the swept wing receives wind from an oblique direction, like during a sideslip, the available air energy will not be lost in the same proportion for each wing (see image on the right, above).
The chord of the right wing is better oriented in the airflow coming from the right, and a larger ratio of air generates lift compared to when the airflow comes frontally. This is the contrary for the left wing. This effect also contributes to lateral stability.
Preventing spiral
The dihedral angle participates to the roll stability, along with other factors. The area where the dihedral plays a critical role is the stabilization of the spiral mode (or spiral divergence).
The spiral mode, like the Dutch roll and the phugoid, is an oscillatory mode that can either self-decay with time (stable) or constantly increase (unstable). The unstable spiral mode happens this way:
- (1) The disturbance creates a small roll moment and sideslip to the right.
- (2) The sideslip creates a crosswind component from the right.
- (3) The vertical stabilizer AoA increases and creates lift to the left.

- (4) Lift creates a yaw moment and turns the nose to the right.
- (1) The yaw moment increases the roll moment and the sideslip to the right (a new cycle has begun).
If this effect is not detected and corrected, which can easily happen in IMC when the natural horizon is not visible, the aircraft continues to sideslip and yaw, while the vertical component of the lift decreases due to the roll, creating a dangerous spiral downwards which can lead to structural damages or ground collision.
The cycle is the result of all dynamic forces in action on the aircraft, in particular the lift on each wing and the position of the center of pressure.
The use of a dihedral wings affects the forces and their relative timing, and transforms an unstable spiral mode into a stable one. This is facilitated by also using a smaller vertical stabilizer and rudder, which in turn can create an unstable Dutch roll, or a shorter cabin.
Thanks to ahmetsalih for the Learjet 3D model available at TF3DM.