Why is there a difference between GPS Speed and Indicator speed?

Question

I just played with flight simulator and noticed that the GPS shows different speed from the speed indicator in the cockpit. Also, GPS speed is higher than the Indicator. Any Idea why?

Answer 1

The speed indicator in the cockpit shows indicated airspeed. Indicated airspeed is usually different than GPS speed, due to wind and aerodynamic effects.

GPS speed is your speed with respect to the ground. If you are standing on terra firma it reads 0. If it reads 100 knots you will be 100NM away from where you are now in one hour, so long as you keep flying in a straight line.

Airspeed is the speed of the aircraft relative to the surrounding air. So if you are standing on terra firma with 20 knots wind blowing in your face, your airspeed will be 20 knots. If you travel at 100 knots airspeed against a 20 knots headwind wind, your ground speed is 80 knots. If you do 100 knots airspeed with 20 knots tailwind, your GPS speed reads 120 knots.

But even in calm wind conditions the airspeed indicator will read differently than the GPS speed . This has to do with the way airspeed is measured.

Airspeed is measured with a pitot tube. A pitot tube has two pressure measurement ports. One that measures the total pressure $P_t$. This port is facing the incoming airflow. The other measures the static pressure $P$ and is placed perpendicular to the airflow. The difference between the two pressures is called impact pressure (pressure rise due to the airflow impacting the pitot tube) and is denoted $q_c$.

The impact pressure is related to the speed of the airflow the pitot tube is exposed to. If the flow is considered incompressible (which is an acceptable approximation for speeds up to 200 knots) the impact pressure can be derived from Bernouilli's equation.

$q_c = \frac{1}{2}\rho V^2$

• $q_c$ is the impact pressure in Pa
• $\rho$ is the density in kg/m³
• $V$ is the true airspeed in m/s

The airspeed indicator is calibrated for standard sea level conditions, where $\rho$ is 1.225 kg/m³. In reality the aircraft will fly at altitude and therefor the actual density of the air is lower. Therefor the indicated airspeed will be lower as well. For example if an aircraft flies 75 m/s (about 146 knots) at 6000 ft the density will be 1.02393 kg/m³.

$q_c = \frac{1}{2} 1.02393 \cdot 75 ^2 = 2879.8 \textrm{ Pa}$

The equivalent airspeed at sea level for the same $q_c$ is:

$V_{EAS} = \sqrt{\frac{2 q_c}{\rho_0}} = \sqrt{\frac{2 \cdot 2879.8}{1.225}} = 68.6 \textrm{ m/s}$

Your airspeed indicator will read only 68.6 m/s (133 knots) despite the fact that you are moving with 75 m/s (146 knots) with respect to the air.

Conversion of true airspeed to the equivalent airspeed can be done directly by:

$V_{EAS} =V\cdot \sqrt{\frac{\rho}{\rho_0}}$

• $V_{EAS}$ equivalent airspeed (m/s)
• $V$ true airspeed (m/s)
• $\rho$ actual air density (kg/m³).
• $\rho_0$ density at standard sea level conditions (1.225 kg/m³)

The effects of the lower density on your aispeed indicator become more pronounced the higher you go. Once you go faster than about 100 m/s true airspeed the effects of compressibility can no longer be ignored and the above no longer applies. Airspeed indicators are corrected for effects of compressibility and therefore don't use the equivalent airspeed but instead use calibrated airspeed for calibration.

$V_{CAS}=a_{0}\sqrt{5\left[\left(\frac{q_c}{P_{0}}+1\right)^\frac{2}{7}-1\right]}$

• $V_{CAS}$ is calibrated airspeed
• $a_{0}$ is the speed of sound under standard sea level conditions (340.3 m/s)
• $P_0$ is the static air pressure under standard sea level conditions (101325 Pa)
• ${q_c}$ is the impact pressure

The impact pressure is also a bit more complex for compressible flow:

$\;q_c = P\left[\left(1+0.2 M^2 \right)^\tfrac{7}{2}-1\right]$

• $P$ the static pressure
• $M$ the Mach number

Effectively, the higher and faster you get, the greater the difference between the indicated airspeed and the true airspeed. For example, Mach 0.8 at 40000 ft in no wind will result in a GPS speed of 489 knots, but a calibrated airspeed of only 242 knots, which is less than half.

Therefore at high altitudes and speeds, the indicated airspeed will be lower than the ground speed / GPS speed, unless you have extreme headwind.

Answer 2

Here's a very simple graphic of what you could be seeing:

_{(source: cadblog.net)}

And this is why we land into a headwind rather than the tailwind, since otherwise we would land at a faster speed and require more runway to stop.

GPS measures ground speed, or absolute speed. The pitot tube on the aircraft will measure the speed relative to the airflow around the aircraft.

Here's som helpful graphic from NASA on relative velocity:

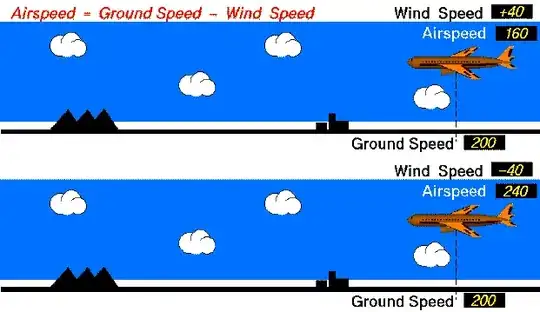
Footnote: As Ratchet Freak demonstrates in his equation, you have to of course remember that this is simplifying it as flying straight into the wind and not taking account of the wind direction.

Answer 3

The other answers about wind are true, but this isn't what you're seeing in your simulation. What you're actually seeing is the difference between true airspeed and indicated airspeed.

True airspeed is the plane's actual speed through the air. With no wind, this is the same as the plane's speed across the ground. This is what your GPS displays.

The airspeed indicator, on the other hand, is really just a "dynamic pressure" sensor. It works by measuring the pressure of the ram airflow. But as we know, as you climb up into the atmosphere, the air gets thinner - less dense, and lower pressure. This makes the airspeer indicator read lower than true airspeed.

The reason it's done this way is because all of the important aerodynamic stuff that can happen to a plane (like stalling) really is tied to dynamic pressure rather than true airspeed.

Answer 4

Gonna try give as simple an answer as possible, but speeds in aviation takes a bit to get your head around....

The cockpit airspeed indicator (ASI) measures indicated airspeed, or IAS, measured in knots. But IAS is technically not a speed at all. It can be thought of as a measurement of the pressure of the air molecules flowing over the wing.

IAS is the most important speed because if the pressure of air molecules going over the wing is too low you'll lose lift and stall. More speed though means more pressure.

At high altitude, there are less air molecules, so less pressure on the wing. Therefore, to keep the same pressure on the wing (i.e to keep the same IAS), you need to go faster. True airspeed (TAS) measures how fast you are actually going. In flight it will be higher than the IAS. TAS does not care about the pressure over the wing - it's the speed through the air.

Groundspeed (GS) is simply the TAS with the effect of wind added. Groundspeed is the speed of aircraft in relation to the ground. If you have a TAS of 200kts, and a tailwind of 50kts your speed over the ground will be 250kts. This is the speed the GPS will show.

Answer 5

Indicated airspeed is an approximation of the plane's speed in the air. Wind can cause the true airspeed to differ from ground speed (what the GPS shows).

To convert it to ground speed you need to know the wind speed and add them.

$$\vec v_{air}+\vec v_{wind}=\vec v_{ground}$$