Why do we need a negative derivative of the pitching moment? restoring moment should be enough?

Question

I am wondering why I read everywhere, that for static stability (longitudinal) the slope of the lift coefficient has to be negative.

Imagine a curve (cm= coefficient of moment , alpha = angle of attack) like the one on my picture. In the trimmed condition where c_m=0 : when I have a an increase in angle of attack, it should be enough, when c_m is negative, because I will always have a restoring moment. The more negative it is, the stronger the restoring moment.

So also when the slope is increasing, I am still in the negative area like in the red area of the picture with a restoring moment.

What I can imagine: such a slope of cm over alpha for a whole aircraftwill maybe not exist?

Thank you for your comments and thoughts

Answer 1

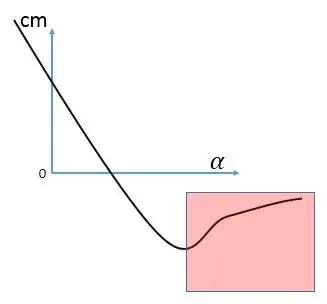
So let’s assume the aircraft has a $C_{m_a}$ curve as you show. When you start to pull up you will feel nose down force on the yoke because of negative pitching moment. As you further increase the pull, the force required should increase also. However in your picture at some point the negative pitching moment $C_m$ decreases (in magnitude), still negative though. That can cause all unwanted motions in the aircraft because suddenly the force you are applying is becoming too excessive. It can even over-g the aircraft depending on the conditions. You are basically braking the linear response of the aircraft.

Ironically enough , that was the main reason Boeing 737 Max was equipped with MCAS in the first place. The stick force per g was not linear at some corners of the envelope. So they put MCAS to linearize the $C_{m_a}$, initially. Of course then they extend it to low speed region also.

Additionally, Part 25 Airworthiness Standards for big aircrafts requires stick force curve slope to have a stable slope:

§25.175   Demonstration of static longitudinal stability.

…

(1) With the landing gear retracted at high speed, the stick force curve must have a stable slope at all speeds within a range which is the greater of 15 percent of the trim speed plus the resulting free return speed range, or 50 knots plus the resulting free return speed range, above and below the trim speed (except that the speed range need not include speeds less than 1.3 $V_{SR1}$, nor speeds greater than $V_{FC}$ / $M_{FC}$, nor speeds that require a stick force of more than 50 pounds), with—

As for the small aircrafts the Part 23 requirement has a little bit of a leeway:

§23.2145   Stability.

(a) Airplanes not certified for aerobatics must—

…..

(3) Provide stable control force feedback throughout the operating envelope.

The part you are asking is specifically addressed in FAA AC25-7C:

§26

...

There may be no force reversal at any speed that can be obtained, except lower than the minimum for steady, unstalled flight or, higher than the landing gear or wing flap operating limit speed or VFC/MFC, whichever is appropriate for the test configuration.

...

(4) Examples of “local reversals” are given in Figure 26-2. Curves A and C depict a local gradient reversal within the required speed range. Even though it might be argued that the “average gradient” meets the one pound in six knots criterion, the gradient reversals would render these characteristics unacceptable. Curve B depicts a situation in which the gradient reverses, but only outside the required speed range. In addition, Curve B demonstrates a situation in which the local gradient does not always meet the required one pound in six knots, even though the average gradient does.

Answer 2

Remember that when you are analysing stability, you are interested in the derivatives by the parameter in question, not in the absolute magnitude. In longitudinal motion, you are mostly interested in how the balance changes when AoA changes. It is understood that in static motion, the absolute moment will be trimmed out (normally by tail) - otherwise it woudln't be static. Stability is usually analysed around a given static point.

On the picture, the derivative is the slope of the curve. Let's break it up in three parts.

• When the curve is above the X axis ($c_m$ is positive, slope is negative), you have a stable situation with positive (pitch-up) moment. This moment will need to be compensated with an additional negative moment from the tail if we are to fly in this region statically. For a classic airplane, this is often a desirable situation because it reduces the trim drag. (But we need to consider the whole system to calculate if it's indeed more efficient).
• When the curve is below X but still has negative slope, everything is the same except that the tail will need to provide an additional positive static moment, often at the cost of negative tail lift.
• In the selected region with positive slope, you have an unstable derivative and pitch-up static moment. Is it that good? If you want to fly in this region, you'll trim out the absolute moment (effectively moving the curve up). Then, as you can see, still any increase in AoA will produce a positive (pitch-up) moment, driving it to further increase AoA.

If the curve represents the moment of a given fixed airplane configuration, the airplane will settle on the crossover point where $c_m = 0$, and we can see which AoA it will have. (By the way, given that $c_m$ is more or less independent of speed, this demonstrates that trim actually sets a fixed angle of attack rather than anything else).

But you are right in the sense that if, again, we consider the situation 'as is', i.e. trimmed and fixed as depicted, the aircraft will still 'slide back' to the stable trimmed point even from the shaded region, just less eagerly. However, if you continue the curve further, it will often cross $c_m = 0$ again, and past there will create a true runaway situation. In many aircraft, it will then bend down again and become stable, crossing the axis for the third time, now with a stable secondary trim point. This is typically a deep stall situation.