Calculate speed by turn angle and distance

Question

I'm trying to combine two rate of turn formulas, which I found it online this and this.

The first is ROT = 1091 * tan(bank angle) / speed in knots

The second is ROT = speed in knots / radius

By combination,

1091 * tan(bank angle) / speed in knots = speed in knots / radius
speed in knots = [1091 * tan(bank angle) * radius] ^ 0.5

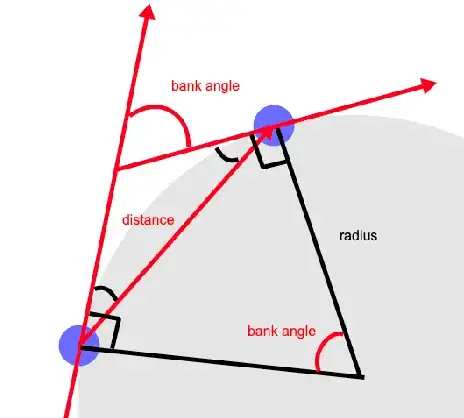
By finding radius, use the simple trigonometry formula c^2 = a^2 + b^2 - 2ab * cos(C)

distance^2 = radius^2 + radius^2 - 2 * radius * radius * cos(bank angle)
distance^2 = 2 * radius^2 * (1 - cos(bank angle))
radius = distance / [2 * (1 - cos(bank angle))] ^ 0.5

Therefore

speed in knots = [1091 * tan(bank angle) * [distance / [2 * (1 - cos(bank angle))] ^ 0.5]] ^ 0.5

Below is the calculation I got. It shows higher bank angle, higher speed and lower turn radius. Does this make sense if the angle-of-attack is fixed? Or I have some wrong calculation? Thanks.

bank angle:     5      10     20     35
distance_in_NM: 2.33   2.33   2.33   2.33
turn_radius:    26.67  13.35  6.70   3.87
speed_in_knots: 50.45  50.67  51.58  54.36

-------------EDIT-------------

The first is still the same. ROT (°/sec) = 1091 * tan(bank angle) / speed in knots

The second is ROT (°/min) = 0.955 * speed in knots / radius. By converting it to °/sec and thanks by Gerry suggestion, ROT (°/sec) = [0.955 * (speed in knots / 60)] / radius

To combine these two formulas,

1091 * tan(bank angle) / speed in knots = [0.955 * (speed in knots / 60)] / radius
speed in knots = [1091 * tan(bank angle) * radius * 60 / 0.955] ^ 0.5

As a result,

speed in knots = [(1091 * tan(bank angle) * 60 / 0.955) * [distance / [2 * (1 - cos(bank angle))] ^ 0.5]] ^ 0.5

Another attempts with different bank angles. Still higher bank angle, higher speed and lower turn radius.

bank angle:     5       10      20      35
distance_in_NM: 2.33    2.33    2.33    2.33
turn_radius:    26.67   13.35   6.70    3.87
speed_in_knots: 399.91  401.64  408.81  430.89

A 3-mile turn radius at 50 knots & 35 degrees of bank looks too large, as does a 26 mile (!!!) turn radius, even at just 5 degrees of bank. I suspect there is a units conversion gone wrong someplace. — Ralph J, Jan 11 '22 at 17:04
The first equation gives ROT in deg/sec. The second gives ROT in deg/min. There's a factor of 60 that needs to be addressed. — Gerry, Jan 11 '22 at 17:31
As described the second equation is an approximation. Consider 60 kts and a radius of 1 NM. In one minute at 60 kts, you would travel 1 NM (along the curve). That would mean an angular change in direction of 1 radian. Since 1 radian is 57.3 degrees. that would less than the 60 deg per minute provided by the equation. More correct would be ROT_in_deg/min=0.955 * Speed_in_Kts / radius_in_NM. You need to devide that by 60 to deg/sec. — Gerry, Jan 11 '22 at 17:46
You should edit your values to properly reflect significant figures Your numbers imply that you are capable of measuring distances with accuracies in the tens of picometers, or millionths of an inch... (relevant xkcd) — randomhead, Jan 11 '22 at 18:28
VTC based on the problems with the question as described in quiet flyer's answer (and @randomhead's comment). — Ralph J, Jan 11 '22 at 19:33
@randomhead You are right cuz I calculate the number by coding. Thanks for your reminding. I adjusted the numbers — Pak Ho Cheung, Jan 11 '22 at 19:49
The pic is not very clear. Is it a top view of an aeroplane flying a coordinated turn? Then, which distance do you want to compute at which specific point in time? How is aeroplane bank angle now an angle determining 2 points on a circle? — Koyovis, Jan 12 '22 at 22:03
If this question gets any more editing then that would be a good time to add the "flight-dynamics" tag — quiet flyer, Jan 13 '22 at 12:09
The issue here is the mixing of units without understanding the need to use all the same units, and ensure that they cancel out. To do that unit conversion constants (like 1 nm = 6080 feet, etc. etc.) must be included. See my answer below. — Charles Bretana, Jan 14 '22 at 15:43

score 4 · Answer 1 · edited Jan 12 '22 at 13:53

If we remain in the SI metric unit system, this answer finds 2 equations:

$\omega = \frac{g}{V} \cdot \tan (\Phi)$
$ \omega = L \cdot \sin(\Phi) / (m \cdot V)$

With $\omega$ in rad/sec.

Equation 1. is for an aeroplane making a coordinated turn, keeping altitude. Equation 2 is not concerned with keeping altitude. Your second equation ROT = speed in knots / radius boils down to V = $\omega \cdot$r, take any V and any r.

So $V/r = g/V \cdot \tan (\Phi)$ finds $$ r = \frac{V^2}{g\cdot \tan (\Phi)} $$.

No need to compute a distance, however a protection against divide-by-zero is required.

quiet flyer · Accepted Answer · 2022-01-11T18:45:12.723

3

Below is the calculation I got. It shows higher bank angle, higher speed and lower turn radius. Does this make sense?

If we specified that angle-of-attack were fixed, so that airspeed increased as a function of wing loading, then it would make perfect sense that banking steeper would result in both a higher airspeed, and a smaller turn radius.

But that doesn't appear to be what you are doing here. You don't have any formula relating to wing loading. You have too many outputs and not enough inputs -- the only input appears to be bank angle. That's not enough information to draw any valid conclusions about airspeed or turn rate.

If turn rate and bank angle were both inputs, then we could compute the airspeed. But that doesn't appear to be what you are doing.

It appears that you need to start over with a fresh "clean sheet" of paper and fundamentally re-think your approach here.

edited Jan 11 '22 at 18:45

answered Jan 11 '22 at 18:36

quiet flyer

22,598
5
45
129

Thanks for the answer. Yea. Assumption for the angle-of-attack is fixed here as I use these formula to make some simulations. – Pak Ho Cheung Jan 11 '22 at 19:50
@PakHoCheung -- I suggest editing the question to include that information-- – quiet flyer Jan 11 '22 at 20:26
@PakHoCheung -- I suspect your analysis may be entirely correct, I haven't gone through it in enough detail to be sure-- you just didn't include all the needed information, in the actual question-- – quiet flyer Jan 11 '22 at 21:17
Edited to include that information. Thanks:) – Pak Ho Cheung Jan 12 '22 at 12:31

Charles Bretana · Answer 3 · 2022-01-14T15:40:16.580

First understand the physics.

Rate of turn (ROT) is the number of degrees of heading change that an aircraft makes in a set period of time. It is measured in degrees per second or degrees per minute. The formula for ROT is simple. It is the radial G divided by the aircraft true air speed.

Radial G is the acceleration in the direction you are turning. It is measured in acceleration units, distance per time squared (say meters per second squared), and Velocity of course is in Distance per time (Meters per second). When you perform this division the meters and one of the seconds units cancel each other, and what you have left is something per second. By definition, this is an angle measured in radians ( approximately 57 degrees ) The first formula you are using

1091 * tan(bank angle) / speed in knots

is derived from the above by assuming level flight (no climb or descent) where the radial G is the horizontal component of the acceleration due to the lift from the wing at a specific bank angle (radial G = tan (Bank angle) * 9.81 m/sec2), and converting knots (nautical miles/hr) into meters/sec.

So One nautical mile is 6080ft and one meter = 3.28 feet so nautical mile is
6080 / 3.28 = 1853.65 meters
But a knot is nautical miles per hour, so to get m/sec we also need to divide by the number of seconds in an hour (3600)
(1 knot = 1853.65 meters/hour / 3600 sec/hour), and then, since the answer would be in dimensionless radians/sec, and we want it in degrees/sec, multiplying by the number of degrees in a radian (57.2958 degree/radian), to get 1091.

9.81 * 3.28/6080 * 57.2958 * 3600 ~= 1091

That's where this formula came from.

The second one is simpler. It is based on the fact that there are 360 degrees in a circle, and that the circumference of a circle is 2 * Pi * radius So if your airplane travels at velocity V (in knots) it will travel completely around the circle (360 degrees), in amount of time = (Distance / Velocity) hours (because we are specifying V in nautical miles per hour). The rate of turn is the number of degrees per unit time, so we just need to divide 360 degrees by that amount of time, and then also divide by 3600 to get from degrees per hour to degrees per second...

 ROT = 360 V / (2 * Pi * radius * 3600)
 ROT = V / (20 * Pi * radius):   
 ROT = V / (62.8318 * radius):   V in knots, radius in nm

This formula is dependent on entering the Velocity in Knots, and the radius in nautical miles. if you want to enter the radius in feet, then you need to convert that as well (one nm = 6080ft) and the formula becomes

 ROT =  96.7 * V / radius:   V in knots, radius in feet

Remember, all of this is only true for an aircraft in a level (no climb or descent) constant bank angle turn). If you are turning in the vertical, the assumptions in this about the radial G required to maintain level flight at a specified bank angle will no longer be true.

Thanks for the explaination. I did wonder how the 1,091 come from. Super clear now — Pak Ho Cheung, Jan 14 '22 at 18:16

Calculate speed by turn angle and distance

3 Answers3