What is the most compact data structure for canonical k-mers with the fastest lookup time?

Question

edit: Results are current as of Dec 4, 2018 13:00 PST.

Background

K-mers have many uses in bioinformatics, and for this reason it would be useful to know the most RAM-efficient and fastest way to work with them programmatically. There have been questions covering what canonical k-mers are, how much RAM k-mer storage theoretically takes, but we have not yet looked at the best data structure to store and access k-mers and associated values with.

Question

What data structure in C++ simultaneously allows the most compact k-mer storage, a property, and the fastest lookup time? For this question I choose C++ for speed, ease-of-implementation, and access to lower-level language features if desired. Answers in other languages are acceptable, too.

Setup

• For benchmarking:
  • I propose to use a standard fasta file for everyone to use. This program, generate-fasta.cpp, generates two million sequences ranging in length between 29 and 300, with a peak of sequences around length 60.
  • Let's use k=29 for the analysis, but ignore implementations that require knowledge of the k-mer size before implementation. Doing so will make the resulting data structure more amenable to downstream users who may need other sizes k.
  • Let's just store the most recent read that the k-mer appeared in as the property to retrieve during k-mer lookup. In most applications it is important to attach some value to each k-mer such as a taxon, its count in a dataset, et cetera.
  • If possible, use the string parser in the code below for consistency between answers.
  • The algorithm should use canonical k-mers. That is, a k-mer and its reverse complement are considered to be the same k-mer.

Here is generate-fasta.cpp. I used the command g++ generate_fasta.cpp -o generate_fasta to compile and the command ./generate_fasta > my.fasta to run it:

return 0;
//generate a fasta file to count k-mers
#include <iostream>
#include <random>

char gen_base(int q){
  if (q <= 30){
    return 'A';
  } else if ((q > 30) && (q <=60) ){
    return 'T';
  } else if ((q > 60) && (q <=80) ){
    return 'C';
  } else if (q > 80){
    return 'G';
  }
  return 'N';
}

int main() {
  unsigned seed = 1;
  std::default_random_engine generator (seed);
  std::poisson_distribution<int> poisson (59);
  std::geometric_distribution<int> geo (0.05);
  std::uniform_int_distribution<int> uniform (1,100);
  int printval;
  int i=0;
  while(i<2000000){
    if (i % 2 == 0){
      printval = poisson(generator);
    } else {
      printval = geo(generator) + 29;
    }
    if (printval >= 29){
      std::cout << '>' << i << '\n';
      //std::cout << printval << '\n';
      for (int j = 0; j < printval; j++){
        std::cout << gen_base(uniform(generator));
      }
      std::cout << '\n';
      i++;
    }
  }
  return 0;
}

Example

One naive implementation is to add both the observed k-mer and its reverse complement as separate k-mers. This is obviously not space efficient but should have fast lookup. This file is called make_struct_lookup.cpp. I used the following command to compile on my Apple laptop (OS X): clang++ -std=c++11 -stdlib=libc++ -Wno-c++98-compat make_struct_lookup.cpp -o msl.

#include <fstream>
#include <string>
#include <map>
#include <iostream>
#include <chrono>
//build the structure. measure how much RAM it consumes.
//then measure how long it takes to lookup in the data structure

#define k 29

std::string rc(std::string seq){
  std::string rc;
  for (int i = seq.length()-1; i>=0; i--){
    if (seq[i] == 'A'){
      rc.push_back('T');
    } else if (seq[i] == 'C'){
      rc.push_back('G');
    } else if (seq[i] == 'G'){
      rc.push_back('C');
    } else if (seq[i] == 'T'){
      rc.push_back('A');
    }
  }
  return rc;
}

int main(int argc, char* argv[]){
  using namespace std::chrono;
  //initialize the data structure
  std::string thisline;
  std::map<std::string, int> kmer_map;
  std::string header;
  std::string seq;
  //open the fasta file
  std::ifstream inFile;
  inFile.open(argv[1]);

  //construct the kmer-lookup structure
  int i = 0;
  high_resolution_clock::time_point t1 = high_resolution_clock::now();
  while (getline(inFile,thisline)){
    if (thisline[0] == '>'){
      header = thisline.substr(1,thisline.size());
      //std::cout << header << '\n';
    } else {
      seq = thisline;
      //now add the kmers
      for (int j=0; j< thisline.size() - k + 1; j++){
        kmer_map[seq.substr(j,j+k)] = stoi(header);
        kmer_map[rc(seq.substr(j,j+k))] = stoi(header);
      }
      i++;
    }
  }
  std::cout << "  -finished " << i << " seqs.\n";
  inFile.close();
  high_resolution_clock::time_point t2 = high_resolution_clock::now();
  duration<double> time_span = duration_cast<duration<double>>(t2 - t1);
  std::cout << time_span.count() << " seconds to load the array." << '\n';

  //now lookup the kmers
  inFile.open(argv[1]);
  t1 = high_resolution_clock::now();
  int lookup;
  while (getline(inFile,thisline)){
    if (thisline[0] != '>'){
      seq = thisline;
      //now lookup the kmers
      for (int j=0; j< thisline.size() - k + 1; j++){
        lookup = kmer_map[seq.substr(j,j+k)];
      }
    }
  }
  std::cout << "  - looked at " << i << " seqs.\n";
  inFile.close();
  t2 = high_resolution_clock::now();
  time_span = duration_cast<duration<double>>(t2 - t1);
  std::cout << time_span.count() << " seconds to lookup the kmers." << '\n';

}

Example output

I ran the above program with the following command to log peak RAM usage. The amount of time the lookup of all k-mers in two million sequences is reported by the program. /usr/bin/time -l ./msl my.fasta.

The output was:

 -finished 2000000 seqs.
562.864 seconds to load the array.
  - looked at 2000000 seqs.
368.734 seconds to lookup the k-mers.
     1046.94 real       942.38 user        78.96 sys
11680514048  maximum resident set size

So, the program used 11680514048 bytes = 11.68GB of RAM and it took 368.734 seconds to lookup the k-mers in two million fasta files.

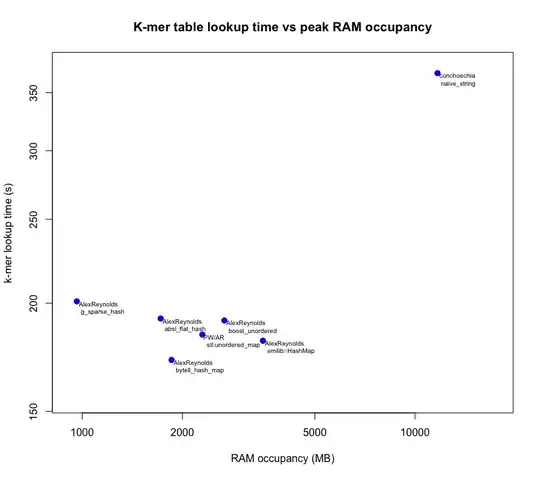
Results

Below is a plot of the results from each user's answers.

Answer 1

The question and the accepted answer are not about k-mer data structure at all, which I will explain in detail below. I will first answer the actual question OP intends to ask.

The simplest way to keep k-mers is to use an ordinary hash table. The performance is mostly determined by the hash table library. std::unordered_map in gcc/clang is one of the worst choices because for integer keys, it is very slow. Google dense, ska::bytell_hash_map and ska::flat_hash_map, tsl::robin_map and absl::flat_hash_map are much faster. There are a few libraries that focus on smaller footprint, such as google sparse and sparsepp, but those can be a few times slower.

In addition to the choice of hash table, how to construct the key is critical. For k<=32, the right choice is to encode a k-mer with a 64-bit integer, which will be vastly better than std::string. Memory alignment is also important. In C/C++, as long as there is one 8-byte member in a struct, the struct will be 8-byte aligned on x86_64 by default. Most C++ hash table libraries pack key and value in std::pair. If you use 64-bit keys and 32-bit values, std::pair will be 8-byte aligned and use 16 bytes, even though only 12 bytes are actually used – 25% of memory is wasted. In C, we can explicitly define a packed struct with __attribute__ ((__packed__)). In C++, probably you need to define special key types. A better way to get around memory alignment is to go down to the bit level. For read mapping, for example, we only use 15–23bp seeds. Then we have 18 (=64-23*2) bits left unused. We can use these 18 bits to count k-mers. Such bit-level management is quite common.

The above is just basic techniques. There are a few other tricks. For example, 1) instead of using one hash table, we can use 4096 (=2^12) hash tables. Then we can store 12 bits of k-mer information into the 4096 part. This gives us invaluable 12 bits in each bucket to store extra information. This strategy also simplifies parallel k-mer insertions as with a good hash function, it is rare to insert into two tables at the same time. 2) when most k-mers are unique, the faster way to count k-mers is to put k-mers in an array and then sort it. Sorting is more cache friendly and is faster than hash table lookups. The downside is that sort counting can be memory demanding when most k-mers are highly repetitive.

---

The other answer is spending considerable (probably the majority of) time on k-mer iteration, not on hash table operations. The program loops through each position on the sequence and then each k-mer position. For an $L$-long sequence, this is an $O(kL)$ algorithm. It has worse theoretical time complexity than hash table operations, which is $O(L)$. Although hash table operations are slow due to cache misses, a factor of k=29 is quite significant. Another issue is that all programs in the question and in the other answer are compiled without -O3. Adding this option brings the bytell_hash_map lookup time from 314s to 34s on my machine.

The C program at the end of my post shows the proper way to iterate k-mers. It is an $O(L)$ algorithm with a tiny constant. The program keeps track of both forward and reverse k-mers at the same time and update them with a few bit operations at each sequence position. This echoes my previous comment "You should not reverse complement the whole k-mer". On the same machine, the program looks up k-mers in 5.5s using 792MB RAM at the peak. This 6-fold (=34/5.5) speedup mostly comes from k-mer iteration, given that the hash table library in use is known to have comparable performance to bytell_hash_map.

---

#include <stdio.h>
#include <stdint.h>
#include "khash.h"

static inline uint64_t hash_64(uint64_t key)
{ // more sophisticated hash function to reduce collisions
  key = (~key + (key << 21)); // key = (key << 21) - key - 1;
  key = key ^ key >> 24;
  key = ((key + (key << 3)) + (key << 8)); // key * 265
  key = key ^ key >> 14;
  key = ((key + (key << 2)) + (key << 4)); // key * 21
  key = key ^ key >> 28;
  key = (key + (key << 31));
  return key;
}

KHASH_INIT(64, khint64_t, int, 1, hash_64, kh_int64_hash_equal)

unsigned char seq_nt4_table[128] = { // Table to change "ACGTN" to 01234
  4, 4, 4, 4,  4, 4, 4, 4,  4, 4, 4, 4,  4, 4, 4, 4,
  4, 4, 4, 4,  4, 4, 4, 4,  4, 4, 4, 4,  4, 4, 4, 4,
  4, 4, 4, 4,  4, 4, 4, 4,  4, 4, 4, 4,  4, 4, 4, 4,
  4, 4, 4, 4,  4, 4, 4, 4,  4, 4, 4, 4,  4, 4, 4, 4,
  4, 0, 4, 1,  4, 4, 4, 2,  4, 4, 4, 4,  4, 4, 4, 4,
  4, 4, 4, 4,  3, 4, 4, 4,  4, 4, 4, 4,  4, 4, 4, 4,
  4, 0, 4, 1,  4, 4, 4, 2,  4, 4, 4, 4,  4, 4, 4, 4,
  4, 4, 4, 4,  3, 4, 4, 4,  4, 4, 4, 4,  4, 4, 4, 4
};

static uint64_t process_seq(khash_t(64) *h, int k, int len, char *seq, int is_ins)
{
  int i, l;
  uint64_t x[2], mask = (1ULL<<k*2) - 1, shift = (k - 1) * 2, tot = 0;
  for (i = l = 0, x[0] = x[1] = 0; i < len; ++i) {
    int c = (uint8_t)seq[i] < 128? seq_nt4_table[(uint8_t)seq[i]] : 4;
    if (c < 4) { // not an "N" base
      x[0] = (x[0] << 2 | c) & mask;                  // forward strand
      x[1] = x[1] >> 2 | (uint64_t)(3 - c) << shift;  // reverse strand
      if (++l >= k) { // we find a k-mer
        uint64_t y = x[0] < x[1]? x[0] : x[1];
        khint_t itr;
        if (is_ins) { // insert
          int absent;
          itr = kh_put(64, h, y, &absent);
          if (absent) kh_val(h, itr) = 0;
          tot += ++kh_val(h, itr);
        } else { // look up
          itr = kh_get(64, h, y);
          tot += itr == kh_end(h)? 0 : kh_val(h, k);
        }
      }
    } else l = 0, x[0] = x[1] = 0; // if there is an "N", restart
  }
  return tot;
}

#include <zlib.h>
#include <time.h>
#include <unistd.h>
#include "kseq.h"
KSEQ_INIT(gzFile, gzread)

int main(int argc, char *argv[])
{
  khash_t(64) *h;
  int i, k = 29;
  while ((i = getopt(argc, argv, "k:")) >= 0)
    if (i == 'k') k = atoi(optarg);
  h = kh_init(64);
  for (i = 1; i >= 0; --i) {
    uint64_t tot = 0;
    kseq_t *ks;
    gzFile fp;
    clock_t t;
    fp = gzopen(argv[optind], "r");
    ks = kseq_init(fp);
    t = clock();
    while (kseq_read(ks) >= 0)
      tot += process_seq(h, k, ks->seq.l, ks->seq.s, i);
    fprintf(stderr, "[%d] %.3f\n", i, (double)(clock() - t) / CLOCKS_PER_SEC);
    kseq_destroy(ks);
    gzclose(fp);
  }
  kh_destroy(64, h);
  return 0;
}