Modelling a Klein bottle

Question

How can you model a Klein bottle, such as this one?

Answer 1

There are most likely several methods, and they probably all have both drawbacks and advantages. I will show how to use the XYZ Math surface for this.

First of all, unless you have already done this, enable the Add Mesh: Extra Objects addon. Go to user preferences (CtrlAltU), click the Addons tab, then Add Mesh. Make sure the check box for Add Mesh: Extra Objects is ticked, then click Save user settings.

Then Add > Mesh > Extra Objects > Math Function > XYZ Math Surface.
This is what you will see

The default object created by this is a snail shell. To get the Klein bottle, enter these equations. Just copy and paste from here.

X equation:

$$-\frac{2}{15}\cos(u)\left(3\cos(v)-30\sin(u)+90\left(\cos(u)\right)^4\sin(u)\\ -60\left(\cos(u)\right)^6\sin(u)+5\cos(u)\cos(v)\sin (u)\right)$$

-2/15*cos(u)*(3*cos(v)-30*sin(u)+90*cos(u)**4*sin(u)-60*cos(u)**6*sin(u)+5*cos(u)*cos(v)*sin(u))

Y equation:

$$-\frac{1}{15}\sin(u)\left(3\cos(v)-3\left(\cos(u)\right)^2\cos(v)-48\left(\cos(u)\right)^4\cos(v)+48\left(\cos(u)\right)^6\cos(v)\\ -60\sin(u)+5\cos(u)\cos(v)\sin(u)-5\left(\cos(u)\right)^3\cos(v)\sin(u)\\ -80\left(\cos(u)\right)^5\cos(v)\sin(u)+80\left(\cos(u)\right)^7\cos(v)\sin(u)\right)$$

-1/15*sin(u)*(3*cos(v)-3*cos(u)**2*cos(v)-48*cos(u)**4*cos(v)+48*cos(u)**6*cos(v)-60*sin(u)+5*cos(u)*cos(v)*sin(u)-5*cos(u)**3*cos(v)*sin(u)-80*cos(u)**5*cos(v)*sin(u)+80*cos(u)**7*cos(v)*sin(u))

Z equation:

$$\frac{2}{15}\left(3+5\cos(u)\sin(u)\right)\sin(v)$$

2/15*(3+5*cos(u)*sin(u))*sin(v)

U min: 0
U max: pi or (3.141592653589793)

V min: 0
V max: 2*pi or (6.28318530718)

U steps and V steps control the number of vertices in each direction, the same as the number of segments and rings on a UV sphere.

If you enable U wrap, the opening of the bottle will be closed. You decide which you prefer. If you enable V wrap, some vertices will be lost, but I haven't been able to find where. I don't know at all what Close V does. It doesn't change either the appearance or the number of vertices and faces.

As you can see, these equations are very complex, and this has the drawback of making them difficult to modify. I will try to show you how to overcome that, using proportional editing and a scaling technique I learned from the answer to my own question in this thread: Making a curved tube thinner or thicker without scaling its overall size

Go into Edit mode, and select all. Remove doubles (W R). Deselect all and make sure Limit selection to visible is disabled.

1. Make sure proportional editing (O) is set to Connected and proportional editing falloff (ShiftO) is set to smooth.

2. Select the vertices you want to modify.
   

3. If you want to make any part of the mesh bigger or smaller, Shrink Fatten (AltS) is the tool. Scroll the mouse wheel to change the size of the sphere of influence of the proportional editing.
   

4. If you want to move any part of the bottle, keep proportional to its aforementioned settings, select the parts you want to move and drag them to where you want them. Like so:
   

5. Repeat steps 2 through 4 until the bottle is to your liking.

You're done.

N.B. A Klein bottle is self intersecting, and therefore won't work as a fluid container with the current fluid simulation of Blender.

Answer 2

Beside math, there can be a simpler way to model it:

• Add Bezier Curve, do not make it cyclic, then tweak points;
• Adjust Radius (Select one or more points, AltS)
• Convert to mesh (AltC - Convert Mesh from Curve/Meta/Surf/Text)
• Bridge the two open loops (W - Bridge Edge Loops)
• Cut off the intersect faces: Mesh > Faces > Intersect, then delete them. (optional)

P.S.:

The consistency of normals has to be broken in this case. It is very interesting, which means you cannot make thickness simply by applying one Solidify modifier. It actually isn't a 3-dimensional thing.

Answer 3

Since it came up in the comments about the normals being a total mess after Remove Doubles is used because the mesh folds through itself I have posted an answer here on how to fix this.
Recently a tool named Intersect was added that can fix this issue by performing what is similar to a Boolean Intersect operation except that this tool works in Edit mode and can handle self-intersections.

The first image shows the messy mesh after Remove Doubles is used.

Now press spacebar and type Intersect and click that entry to activate the tool and change the menu entry to Self-Intersect.

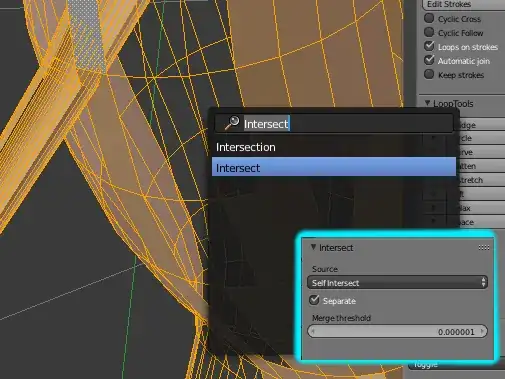
Next use Remove Doubles again. This may require an adjustment to the Merge Distance.

Once that's done you can select everything and use Ctrl n to Recalculate Normals and it should look good.(aside from the quads meeting up with nGons.)

There are also some interior faces created at the junction which should be deleted.

Here's the result rendered with a glass shader and a bit of volume.