How do you avoid Domain errors, and floating point Not-A-Number or infinity errors in shader node math?

Question

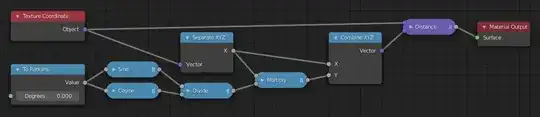
I suppose this applies to Geometry nodes as well, but the problem came up while I was creating a procedural material. I'm trying to animate a material that mimics the rotating line on a radar. For this material, I need the point slope form of a line, but the points derive from polar coordinates. The problem in this instance is that the equation I need takes the form $$ y = x \frac{sin(\theta)}{cos(\theta)} $$

In the animation, $\theta$ is a function of frame and, of course, $cos(\pi/2)$ is 0, leading to division by 0. This is not a good thing.

Other than trying to arrange drivers to avoid multiples of $\pi/2$, how do I deal with potential domain, Not-A-Number (NAN), or infinity situations in shader math?

EDIT: The solution suggested by John MC in the comments and given in detail by Markus von Broady in his answer does work for this specific case.

But it's not a general solution of NANs. I now suspect that there simply isn't a general solution and one simply has to know the potential domain errors that can come come up and code around them.

EDIT 2: Markus von Broady pointed out that NaN isn't the correct term for the problem I'm trying to solve so I've expanded the phrase to include Domain errors and infinities.

This becomes a bit difficult to follow because Domain errors occur in the mathematics, but NAN and infinites are artifacts of floating point implementations.

Answer 1

Sorry if this is not an answer to your more general question, but, following up on your commentary, this sort of arrangement will rotate a line of constant thickness about the origin of your texture space:

... and contains no divisions.

Answer 2

I think I reproduced the gist of your problem:

This node setup uses division of sine by cosine, where the cosine sometimes outputs 0, to calculate a slope (or rather a point on that slope, using current X and calculating Y as in question), then using that to draw a line. When dividing, the smaller the divisor gets, the higher the result is; as the divisor approaches 0, the result gets really damn big (trying to avoid mathematical controversy here). But then, dividing by 0 is undefined, and it can be anything [checked and in Blender the result is 0, see my other answer]: my tests resulted with 0 for 90° and 270°, but something else for 630° (270°+360°) [that's probably the cosine not resulting with exactly 0 due to float unreliability]. The effect is you can get a sudden change from a very big value to 0 which generates something that breaks the pattern, whatever the pattern is (here: a rotating line):

If instead of rendering 360 frames for a 1 second animation, you rendered 360 million frames and used video software to condense that back to 360 frames, the effect wouldn't be noticeable. Likewise, if you're not basing the angle on the time, which almost always has low resolution in software, but use coordinates instead, you don't get this effect:

You need either a terrible luck to hit the sweet spot or force the situation by e.g. rounding the coordinates:

Even then increasing the sampling rate from 1 (above) to default 16 for Eevee viewport (below) will mostly hide it (well at least if the lines breaking the pattern are mathematically thinner than 1 px...):

Going back to the frame driven angle setup, the solution is to check if the value is 0, if so, add a very small value to make it non-zero, or otherwise handle this special case:

Perhaps you want to make the Epsilon slightly larger than 0 as well, though a very small value e.g. 0.00001 would still display as 0 on the screenshot.

Finally, the 90° doesn't break the pattern, but the line still disappears - which is the pattern because it was getting thinner and thinner, which is the flaw of this setup, not sure about yours... To draw a rotating line I suggest a setup like this:

Answer 3

General solution to NaN

Since there is no "NaN" value in Blender shaders (unlike in some programming languages like Javascript), you can't check if a value is "NaN" (like .isNaN() in Javascript). In fact, if you look into Blender's source, the Math node uses safe_divide function, which returns 0.0 when you try to divide by 0:

float safe_divide(float a, float b)
{
  return (b != 0.0) ? a / b : 0.0;
}

So the problem isn't really "how to deal with NaN" - it is "How to deal with special cases". And since special cases are arbitrary, you also have to specifically deal with them on a case by case basis. Not only that, as there is no interface supplied to allow you to deal with them (e.g. the safe_divide function doesn't return a bool + float struct, where the boolean informs you if the float is a special case) you have to investigate what can cause this special behavior and "branch" the logic based on those inputs generating special values or not; therefore the most general solution I can come up with is this:

(to be perfectly clear, you perhaps want to add 0 to that color value so it's a single scalar value again)

Again, it's not really "NaN", just sticking to OP's convention.

Answer 4

In summary, the answer appears to be:

1. If the problem originated as a mathematical domain error, such as division by zero being undefined, look for a different formulation of the math that avoids the problem, as demonstrated by Robin Betts' answer where he substituted a dot product method.

2. If the problem originates as a floating point issue, code around it, as suggested by John MC in a comment and fleshed out by Marcus von Broady in his first answer.

3. Fudge your math to avoid running into the issue as suggested by me in the original question.

4. or simply cope, as the math functions are coded to return (sometimes bad) substitution values rather than fail, and sometimes you can get away with ignoring the problem

I've upvoted the two answers that contributed to the solution, but will be accepting this one because it contains all of the (so far known) approaches.