How to switch beetwen two or more textures with material nodes?

Question

this is a continuation of the previous question, in case you need more context of the problem: How to use the vector of another different object as information for material node?

To sum up: With the help of the answers, I setup two empties and one plane to make it always face the camera and switch texture based on the angle (Like the enemy in the Doom 1993 game).

The empties and plane The material node This setup works with only two images for now.

In one of the answers was mentioned about placing more textures in one single plane and being able to switch between them using material nodes.

1. How can I set up my nodes to work so that every 45° of rotation it switch to the next texture (Right now it has only one "greater than" node with threshold of 0.924 or cosine of 22.5°, use a color ramp perhaps?)
2. What can you do to switch between more than two textures with mix color since they have only two inputs (or what is the correct way to do in case mix color is not the answer?)

Is it possible to set up a working "Doom guy" that rotate and billboard using only one plane and 8 images?

Here's the blend file without images:

Answer 1

Rather than rendering out 8 pics of Suzanne, I'll demonstrate with 8 different colors. I think you understand how to plug images in lieu of those colors....

So the first thing that I/you did here was to take the absolute of the dot product and compare it to the cosine of 45 degrees. Basically what we were doing was saying, we want to know if the angle between the vectors was less than 45 degrees or greater than 225 degrees (that was what the absolute was doing.) Because here, we are now treating the front and back differently, we no longer want the absolute value; because now, we're not particularly interested in 45 degrees, we don't want to compare against a constant like that.

The arccosine of the dot product of two normalized vectors is the angle between them. In radians-- first thing we'll do is convert that to degrees by multiplying with 180/pi. If we divide 360 degrees into 8 angles, we have 45 degrees assigned to each pic. We'll first be interested if our angle is <22.5 degrees (the front is centered on the 45 degree angle), then if our angle is <67.5 degrees, then if our angle is <112.5 degrees.

You'll notice I oriented that going down; rather than testing to make sure they're in range (both less than 67.5 and greater than 22.5) I'm just going to overwrite on the basis of the less-than.

So each of those Mix nodes is fed from the last. We start with red, the color I've labelled "Back"; then if the angle is less than whatever, we overwrite it with BackL; then if the angle is less than whatever, we overwrite it....

But that's only five colors-- only one side. You want eight colors. We need another side. First, let's duplicate this structure that we have, but with some new colors for the right side:

Notice that we're using the same colors for front and back. Doesn't matter what side we're on, front is still front and back is still back. But we still need to know which side we're on the mix between these two.

We can't tell which side of the object we're on from the dot product. We need another vector to do that. We can take the cross product of our two vectors to create a new vector orthogonal to both, and then look at which way our new orthogonal vector is pointing, in order to mix between sides:

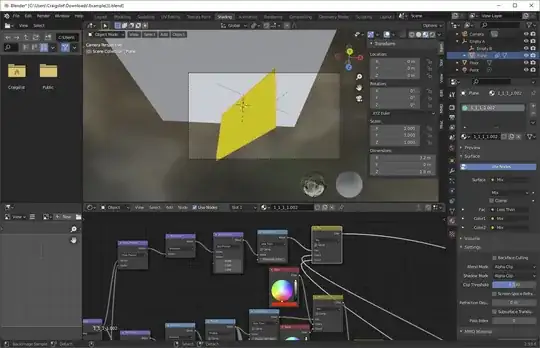
Only thing left is to test it out. Looks right to me: