Unfold cylindrical object around rotation axis

Question

Good evening!

Sometime ago i asked a similar question but i did not get the right answer and the discussion went into a wrong direction. Maybe i did not express myself correctly.

That's why i did a new graphic to clearify my question:

I am part of a project which wants to build a DIY rotational 3D-printer. One current problem is the slicing pipeline. Since we do not have a rotational slicer, we want to unfold a rotational 3D object, slice it with a traditional slicer and do some post-processing (like transforming to rotational coordinates).

That is why i am searching for a transformation function which "unfolds" a (maybe complex) cylindrical object along its rotational axis. Here the distances between two points on the surface (and also "inside" the volume) have to be the same in both objects. Otherwise the amount of extruded filament will to less. With every new layer this error increases and the printed object is not usable.

I found a related post here. But they don't keep the circular length of the layers and only unfold the cylinder with edges orthogonal to the resulting planes.

Does anybody know how I could achieve my transformation or knows how it is called? I have asked and searched a lot but did not find anything which worked the way i need it.

Or is there maybe a better place to ask my question?

Best regards!

Answer 1

Following, I will describe, how to do the conversion that is displayed in your sketch. As I am not experienced in 3d-printing, this does not take into consideration, if it is applicable to 3d-printing (see the answer of Nathan concerning a discussion about that).

We start by converting the points of the cylinder into the cylindrical coordinate system. As stated in Wikipedia,

For the conversion between cylindrical and Cartesian coordinates, it is convenient to assume that the reference plane of the former is the Cartesian xy-plane (with equation z = 0), and the cylindrical axis is the Cartesian z-axis.

Assuming further that x points to the right and y to the top of your sketch, we can compute the cylindrical coordinates as follows:

$$ r = \sqrt{x^2+y^2} $$

if $y \ge 0$ and $r \ne 0$: $$ \varphi = arccos\left( \frac{x}{r} \right) $$

if $y \lt 0$ and $r \ne 0$: $$ \varphi = -arccos\left( \frac{x}{r} \right) $$

To make it easier for me, I will assume, that the dotted line is on the right side of the cylinder and not on the bottom. Then - assuming radial angles - we can calculate the transformed object by:

$$ x’ = 2\pi r \cdot \frac{\varphi}{2 \pi} = r \cdot \varphi $$

For $y \ge 0$ and $r \ne 0$ we get: $$ x’ = \sqrt{x^2+y^2} \cdot arccos\left( \frac{x}{r} \right) $$

And for $y \lt 0$ and $r \ne 0$ we get: $$ x’ = - \sqrt{x^2+y^2} \cdot arccos\left( \frac{x}{r} \right) $$

$y'$ can be calculated by $$ y’ = r = \sqrt{x^2+y^2} $$

And $z'$ simply is: $$ z’ = z $$

Implementation in Geometry Nodes

Because joojaa asked for an implementation in geometry nodes, here it is:

To enable the transformation, we first have to cut the cylinder:

Having done this, we can transform the cylinder:

The group node looks like this:

Answer 2

I mentioned this in a comment, but I realized what I wrote could be interpreted a couple different ways, so I want to be more clear.

If somebody was doing this for rendering, André Zmuda's answer would be great. There are distortions involved, but they're distortions that we can undistort.

But you want to do this for 3D printing, and the distortions are probably not acceptable in your case. This goal for all distances to remain the same is impossible. It is the same problem as trying to UV map a sphere onto a flat plane, the same problem as trying to create a map of the world without any distortions.

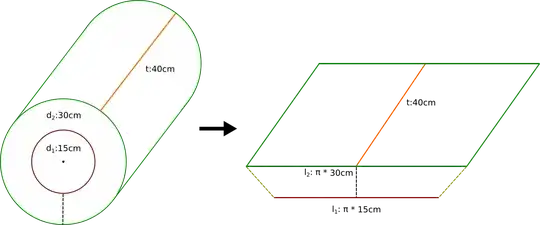
Let's look at our cylinder and mark a few points of interest:

Now lets unwrap your cylinder as you've indicated, just a cross section, and see roughly where we want those points to map:

The bottom line is longer, because it corresponds to the outer circumference, like your picture except upside-down because I wasn't looking at it :) and the outer circumference is longer than the inner circumference, so our cross section is a long trapezoid.

On our cylinder, the shortest point between A and B was through the radius of the cylinder. But now these are angled, and B is actually closer to C than it was to A. By making this a trapezoid, we're turning what was a straight line between two circles-- the shortest path-- into what is now an angled line between two parallel straight lines. That angled line can never be the shortest distance.

Maybe you think there are some transformations that we could do to these points to get the distances back. Let's consider them.

First, we could scale A in toward the middle. But that's getting rid of the differences between our inner and outer circumferences-- that fixes the AB distance only at the point that our trapezoid becomes a rectangle. You've already indicated that this isn't what you want (and indeed, distances are not preserved in this shape either.)

What if we moved A toward B? Then we're no longer preserving the distance between A and C along the outer circumference.

Maybe we could move C further away, so that A became closer? Among other problems with this, this also no longer preserves the distance between A and C. (There are also an infinite number of points between A and C, and B being closer to any of those points isn't any better.)

What about B? Could we move it closer to A? When we move B closer to A, our inner circumference gets bigger to reach B. Again, we distort the inner/outer circumference, and AB doesn't become the shortest path until B gets all the way on top of A.

What if instead of using a trapezoid, we curved our circumferences? As we curve them, AB gets smaller as BC gets larger. How much curvature would we need to get this right? Exactly as much as it takes to make our original cylinder. We can curve the lines to fix the problem, but now it's no longer any mapping at all.

What's that mean for 3D printing? It means that any mapping of this sort will have to involve compression and/or stretching to roll your flat shape up into a cylinder. There is no way to preserve distances with this mapping.

Are there any mappings that can do this without distortion? There kind of is, but it's not much like your image, and it's also not possible in the real world. Just as in UV mapping we make tradeoffs between seams and distortion, we can make tradeoffs here. We can add more seams, at which point distortion decreases. But those seams need to cut through the volume. Your cross section would start by looking like this:

The inner and outer circumference reach the same bounds. The inner circumference is shorter only by virtue of the triangular cutouts.

That's not enough density of cuts to do a distortion free mapping, but it's a start. When you have a box with an infinite number of these cutouts, each infinitely thin, you have a distortion free mapping. That "infinity" is why it's not possible in reality. Again, this is a lot like UV mapping a sphere. We can get a distortion free unwrap, but only when we've seamed nearly every edge, and even then, only because it's not a real sphere, just a sampled sphere (and indeed, if we are working with a sampled cylinder, we could get away with a finite number of cutouts, depending on our sampling.)

But I don't think that mapping is very practical for 3D printing-- even sampled, our outer circumference has points (lines, in 3d) where it is infinitely thin-- and it's certainly not the mapping you had in mind.