Python: vertex normal according to World

Question

If i get a normal of a vertex - i'll get it in local coordinates. For example:

bpy.context.object.data.vertices[0].normal

If an object will have rotation or scale - normal direction will be incorrect according to world orientation. How to convert the vertex normal according to the world?

Answer 1

Normal Matrix.

EDIT. Original answer did not allow for non-uniform scale. Have added a script to reinforce the answer of @patmo141_

Create a normal matrix

$$n' = (M^{-1})^{T} \cdot n $$

as in script below

mw = ob.matrix_world
N = mw.inverted_safe().transposed().to_3x3()

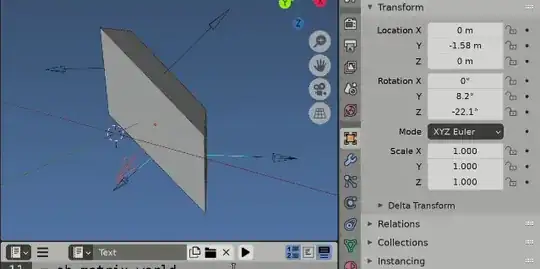
Test script, adds a single arrow type empty at each face normal aligned with face normals in global space.

import bpy
from mathutils import Matrix
norm_length = 2
context = bpy.context
bpy.data.batch_remove((o for o in context.scene.objects if o.type == 'EMPTY'))
ob = context.object
mw = ob.matrix_world
N = mw.inverted_safe().transposed().to_3x3()
for f in ob.data.polygons:
    n = N @ f.normal
    mt = bpy.data.objects.new("n{f.index}", None)
    mt.location = mw @ f.center
    mt.rotation_euler =  n.to_track_quat().to_euler()
    mt.empty_display_type = 'SINGLE_ARROW'
    mt.empty_display_size = norm_length
    context.collection.objects.link(mt)

Note, using face normals as example, for vertex normals as per question

for v in ob.data.vertices:
    n = N @ v.normal
    mt = bpy.data.objects.new("n{f.index}", None)
    mt.location = mw @ v.co

Without inverting.

Using the technique outlined in Stop Using Normal Matrix

\begin{align*} \vec{N'}&=\frac{N_0}{a}\vec{X} + \frac{N_1}{b}\vec{Y} + \frac{N_2}{c}\vec{Z}\\ &=(\frac{N_0}{a}, \frac{N_1}{b}, \frac{N_2}{c})M \end{align*}

Test script,

• Get the scale vector vector s
• Normalize the rotation part Matrix M
• There's an issue where negative scale flipping result
• make a vector n from normal by dividing each component by scale component
• post multiply by M to obtain result normal

edit to above: (remembering to import Vector from mathutils)

M = mw.to_3x3().normalized() 
s = mw.to_scale()
for f in ob.data.polygons:
    n = f.normal
    n = Vector((n.x / s.x, n.y / s.y, n.z / s.z))
n = n @ M

Zero scale component.

Both these methods will have issues when any scale component is zero. The use of inverted_safe will avert risk of divide by zero error at cost of result accuracy. Will look into this.

From the bmesh directly.

As noted in answer to [link] could also apply the transform to a bmesh and update its normals. Tnen the face normals of the bmesh the calculated normals. (The mesh is not updated or written back to)

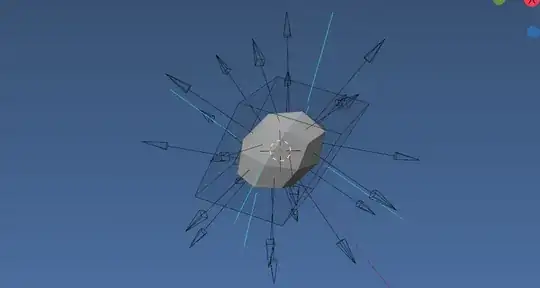Empties added at world coords to mimic normals of evaluated mesh

import bpy
import bmesh
from bpy import context
norm_length = 2
bpy.ops.object.mode_set()
bpy.data.batch_remove((o for o in context.scene.objects if o.type == 'EMPTY'))
ob = context.object
dg = context.evaluated_depsgraph_get()
bm = bmesh.new()
bm.from_object(ob, dg)
bm.transform(ob.matrix_world)
bm.normal_update()
for f in bm.faces:
    n = f.normal
    mt = bpy.data.objects.new("n{f.index}", None)
    mt.location = f.calc_center_median()
    mt.rotation_euler =  n.to_track_quat().to_euler()
    mt.empty_display_type = 'SINGLE_ARROW'
    mt.empty_display_size = norm_length
    context.collection.objects.link(mt)
bpy.ops.object.mode_set(mode='EDIT') 

Answer 2

Actually it is, when the scaling factors are not the same (as @mifth pointed out) :

normal_local = C.object.data.vertices[0].normal.to_4d()
normal_local.w = 0
normal_local = (C.object.matrix_world @ normal_local).to_3d()

If you know they are all the same, you can use :

C.object.rotation_euler.to_matrix() @ C.object.data.vertices[0].normal

Cheers,

Answer 3

I've run into this problem many times, I always have to search for the answer. But I use the tranpose of the inverse of the world_matrix to get the world normal.

https://computergraphics.stackexchange.com/questions/1502/why-is-the-transposed-inverse-of-the-model-view-matrix-used-to-transform-the-nor

mx_inv = C.object.matrix_world.inverted()
mx_norm = mx_inv.transposed().to_3x3()
world_no = mx_norm @ C.object.data.vertices[0].normal

Answer 4

you have to multiply it with the world matrix (the order matters! Matrix first) :

C.object.matrix_world @ C.object.data.vertices[0].normal