3

In other words, I want to bend my mesh along the X axis only at the curve points.

enter image description here

To achieve this, I cut it and then use Robin Betts's X Curve Deform group.

enter image description here

It works great, but it also deforms the mesh in the Y axis where I don't want it to. Or rather, in a way I don't want it to. How can I fix this?

enter image description here

0 - what I get

1 - what I want

quasarnova
  • 45
  • 1
  • 5
  • I think it needs to do that, or if not the side edges length won't stay the same as the original. – lemon May 04 '23 at 15:12
  • Can you describe the way you do want the Y axis to look? – Robin Betts May 04 '23 at 17:06
  • @RobinBetts Oh, sure. See Edit. – quasarnova May 04 '23 at 17:58
  • 1
    note that a curve modifier will also give 0 (what you get and dont want). – lemon May 04 '23 at 18:00
  • @lemon Yeah, I know it. I'm not saying that the group works somehow wrong. I just need a different result. – quasarnova May 04 '23 at 18:05
  • 2
    Yes, I think we understood that. I did something like that in another world https://www.youtube.com/watch?v=KbynGkgh9k8&t=39s .Though, in a nowdays context do you need to "array" the base shape? – lemon May 04 '23 at 18:06
  • @lemon This really looks like what I want. And no, I don't need an array. – quasarnova May 04 '23 at 19:49
  • @quasarnova, in the video this was possible only because the object is arrayed. If not there is no delimited domain that allows the calculation you want (imho). – lemon May 06 '23 at 10:17
  • I want to thank you for asking this, otherwise i might not have figured this out. I got an idea while reading this and it led to a solution. I'll post the answer shortly. – shmuel May 22 '23 at 01:36

1 Answers1

4

Update: 2023-12-27

I actually figured it out! about a month ago. I should post it sometime within the next couple weeks.

What took me the longest to figure out was how to do "even thickness" properly, but I figured it out in the end (when revisiting the problem, in a flash of realization).

Update: 05/28/2023
Until now I posted an implementation that only solved the initial questions problem - which is the interpolation err between points caused (mainly, and in this case only) by the normalization of the attributes (normal). -
I have now also implemented a version that adds 'even thickness' functionality which is important in some situations (but not all, because of the issue that arises at high angles). - happens to be this wasn't so easy to do in three dimensions due to the fact that the normal isn't facing in the directions of angles anymore, so you have to introduce another vector etc.
...but i think i managed to figure it out and will share it some time soon (i did finish it a couple of days ago, but got sidetracked with some trig).

Update: 05/24/2023
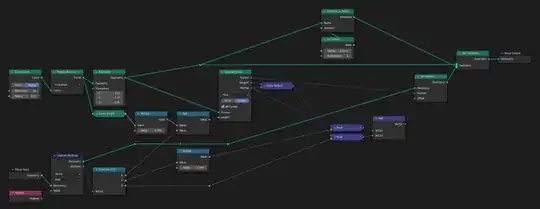
Here is a polished file example:

I'll get around to explaining it some time. There are frames with some notation, so that's something.

update: 05/22/2023
I'm still looking into it. The issue is that the normal is being normalized after being interpolated, which you don't want. you want a linear interpolation between each point. (, so you can just sample the normal through the value socket instead of the normalize output).

This is relatively easy to fix for flat curves, however 3D curves face some more issues. The Tangent is being interpolated and causes some bending, but if you constructed an accurate Tangent you don't get good corners when the curve isn't flat.

Basically I've found various different ways to fix this and am still tooning it.

Original post:
here is a file. I'll write it up better later.
this is the same file as in the question with a solution implemented. It's not a polished solution (though, i do have some) it's there to show that it's fixable with an inclination and foundation to fix it. I'll keep updating with more (and polished) solutions and explanations.

shmuel
  • 1,560
  • 10
  • I'm only using a flat circle, so this makes things easier unless you want to improve your solution for everyone. Anyway, thanks for your time and your answers. – quasarnova May 23 '23 at 06:54