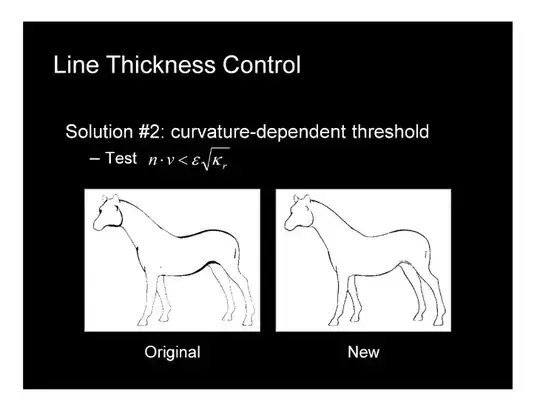
Lets re-visit the variables:
$\textbf{n}$ = Geometry (Normal) Yes, the normal of the surface point.
$·$ = Vector Math (Dot Droduct) Yes.
$\textbf{v}$ = Geometry (incoming) I believe you mean the right thing. It's the view vector from the camera to the surface point.
$\epsilon$ = Threshold Value Yes.
$\kappa$ (small kappa) the common character for curvature. There are different definitions of curvature, but in general it describes how strongly the surface is "not flat" at some surface point. Depending on the complexity of the definition one can express properties like convex/elliptic ($\kappa > 0$), concave/hyperbolic ($\kappa < 0$) and flat ($\kappa = 0$), see Gaussian curvature for example. The radial curvature is never negative ($\kappa_r \geq 0$) because the radius of a sphere (circle in 2D), which approximates the surface point's surrounding is used. For a flat spot the sphere would have infinite radius, thus $\kappa_r = \frac{1}{r = \infty} = 0$. For a very bend surrounding the sphere would be very small and $\kappa_r \gg 0$.
To implement this effect in Blender, i found this very nice post which sets the curvature value of every vertex as its weight. These values can then be accessed in shaders ultimatively, like demonstrated in another very nice post. Use the Camera Data and Geometry node to get $\textbf{v}$ and $\textbf{n}$ in the shader. With all the data at hand, you should be able to implement the formula and achieve the effect. But well, this will be a bit of work.