OK to prove I understood my lesson, I'll also write an answer.
Basics
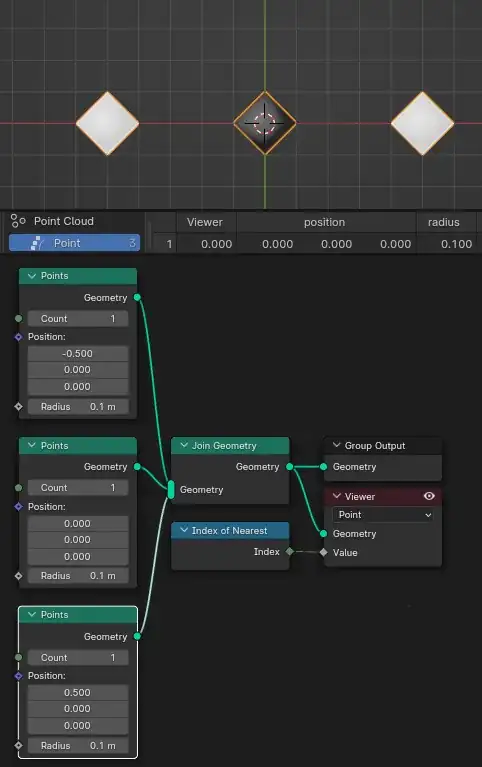
First a simple case just showing how the "nearest index" works in principle: it returns the index of the nearest element, not counting self.
You can see the 1st point, index #0, is on the left; the viewer displays $0$ as black.
The 2nd point (index #1, but it's irrelevant) is in middle and is controlled on the GIF. Only the value evaluated for this point is of interest in this presentation, so you can ignore the colors of other points. For the same reason, the spreadsheet shows only this point.
Finally, the 3rd point, index #2, is on the right; the viewer displays $2$ as white.

For the most part, the result of this experiment is very simple to understand: as the middle point moves to the left, the left point becomes the closer one, and so the middle point reports $0$ (the index of the left point) as the closest index and so becomes black. When the middle point moves to the right, it reports $2$ as the index of the nearest (right) point, and becomes white.
Tie-breaker
However, when the middle point is at an equal distance to both other points, there's no valid answer on which of the two (in this case two; there could be more than 2 ex æquo winners) is closer. Usually the last sorting criterion is index, and so it's reasonable shmuel assumes here also the index is a tie-breaker, but at the same time is surprised the convention doesn't follow in the ascending/descending matter, and in the question the maximum index is picked.
Never assume. This is why I decided to investigate too.
In the GIF above, the point in middle, when it is in perfect middle, becomes black, so it picks the lowest index ($0$). Therefore the tie-breaker is not index.
At the same time we can say the tie-breaker is stable, deterministic, because when the point moves along $y$ axis, remaining at an equal distance to two other points, it remains black instead of blinking, proving the tie-breaker consistency:
I'm too lazy to read the Blender source - perhaps some kind of list of candidates from BVHtree is being processed, and once no more elements can be removed from the list, as all are at an equal distance to the evaluated point - the first element on the list is picked. If you think this could depend on order of sectors of the 3D space, rather than order of the elements, but the below experiment disproves it as well:

The tie-breaker could be something very technical like an ordering based on a hash of each element, so I think it's fair to just call it (deterministic) random…
Radius
Gordon [why did you delete the answer??] introduced various radii in his points, so I just had to test this:

Radii are irrelevant. Points are dimensionless, and radius only affects how a point is displayed, not how close it is considered to be to other points. [Just to be clear: Gordon didn't claim radii are relevant to distance calculation, he used it for a different purpose].
The actual answer
I suspected it, but didn't say so because I didn't want to suggest the answer I didn't want to hear… It doesn't work like "Sample Nearest", that allows a point to override the sampling position (from the default, self position), without affecting self position. Think about it, if you were sampling the same geometry from which you are sampling, and overriding the default "Position" input from current position to anything else, you would move the points rather than say from where you're sampling, and so you would always find yourself. Of course the flaw of this argument is that it's never "the same" geometry, as logically (an implementation may be different but will act as if this statement was true) geometry is passed by value, not reference - each link makes a copy of geometry.
Here's two equivalent setups:

And so the "Position" input serves as a convenience feature that can save you up to 5 nodes, if you actually need to move those points, need that to be temporary, don't store the position for other reasons etc.
Proof
Here's an expensive way to produce an empty geometry:


For a 1000 tries, a 1000 points with random positions, overridden to other random positions, found the same connection, so I think this proves those setups are equivalent.
The Misconception
This is how I actually thought this works:

You may think: it would be a convenience feature for a similar number of nodes. There is however a crucial difference: in this case, these nodes are run as many times as many points there are. So if you have a completely reasonable number of 10 000 points, the algorithm could be maybe 10 times slower in the first case, but 10 000 faster in the second case. I understand, however, that it wouldn't be easy to implement it this way.









