Is [Co(NH₃)₄Cl₂]Cl paramagnetic or diamagnetic?

Question

$\ce{NH3}$ is known to be a strong field ligand, while $\ce{Cl}$ is known to be a weak field ligand.

Is $\ce{[Co(NH3)4Cl2]Cl}$ a high spin complex or a low spin complex?

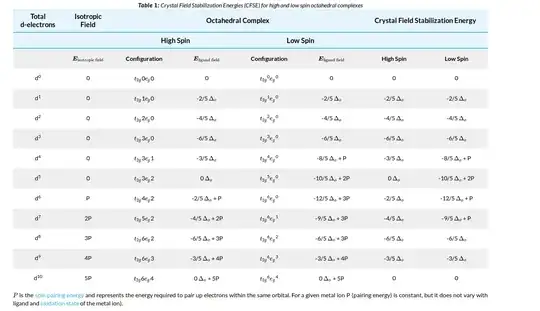
I assumed this to be a high spin complex. Oxidation state of $\ce{Co}$ is $+3$. And electronic configuration of $\ce{Co(III)}$ is $\mathrm{[Ar]~3d^6}$.

Since I assumed this to be a high spin complex — pairing of electrons of $\mathrm{3d}$ orbitals will not happen. The $6$ pairs of electrons from the ligands must be included in the $\mathrm{4s}$, $\mathrm{4p}$, $\mathrm{4d}$ orbitals — which leaves electrons unpaired in the $\mathrm{3d}$ orbital, making this a paramagnetic complex, with hybridisation $\mathrm{sp^3d^2}$.

Answer given to this question says otherwise. Hints are welcome!

This question is an excerpt of a question that appeared in the JEE(A) - 2016

Answer 1

The point is not really whether chloride or ammonia is a strong or weak field ligand, the point is $\ce{Co^3+}$ is $\mathrm{d^6}$, and virtually all "octahedral" $\mathrm{d^6}$ complexes are low spin - essentially some complexes of $\ce{Fe^2+}$ and a very small number of fluoro complexes of $\ce{Co^3+}$ are the only exceptions to the rule that all $\mathrm{d^6}$ octahedral complexes are low spin.

Why is this? Well let's use a bit of Crystal Field Theory (much of below stolen from https://chem.libretexts.org/Bookshelves/Inorganic_Chemistry/Supplemental_Modules_(Inorganic_Chemistry)/Crystal_Field_Theory/Crystal_Field_Stabilization_Energy). One can consider the crystal field stabilization energy which is how stabilized an ion is compared to the free ion when in a given electronic state electronic and geometry. Here we are interested in high and low spin, and octahedral geometry. Taking a table of these values from the above link:

In the above $\Delta_\circ$ is the splitting energy of the orbitals. We can see that low spin $\mathrm{d^6}$ has the largest possible stabilization energy of any electronic configuration compared to the high spin case ($2\Delta_\circ$-P). Thus unless the splitting is very small octahedral $\mathrm{d^6}$ prefers low spin. So how do we get small splitting to see high spin $\mathrm{d^6}$? Well small splitting is favoured by

• Low charge first row transition metals - for instance $\ce{Fe^{2+}}$
• Very weak field ligands

And what were our exceptions above?