An autocatalytic reaction is a reaction in which one of the products catalyses the reaction.
In general what will be the shape of curve if the rate of reaction was plotted against time for an autocatalytic reaction?
I think answer should be A (in image) as an autocatalyst should always increase rate of reaction until there is a limiting factor for example concentration but the answer is B.
As Curt F. has correctly showed that, in general, if the rate of reaction is plotted against time for an autocatalytic reaction, it would be the shape of curve B (in your question). Since Curt F. has already worked with the mathematical part, only I can do is show you some literature evidence. One of research on an epoxy resin composite hardening (Ref.1) state that:
Composite structures for aerospace applications are mainly made by the well-known prepreg technology. In order to achieve adequate prepreg processing schedules, and consequently maximum fiber strength utilization, one has to know in deep the cure kinetics of matrix, which held the fibers together. This work describes a procedure to study the cure kinetic and has as example how aromatic amine hardeners influence the cure kinetics of an epoxy resin used in advanced composites. The investigation was carried out by using the DSC technique and it was found that depending on the system used the cure kinetics of the formulation obeys order $n$ or autocatalytic order.
For Comprehensive details for autocatalyzation and review, see Ref.2 & 3.
References:
Let's suppose the mechanism is:
$$\ce{A + B <=> (AB) -> B + B}$$
Here, A is decomposed catalytically by B into B through the formation of a transient (AB) complex.
We can decompose two-step process into two reactions:
$$\ce{A + B <=>[k_1][k_2] (AB)} $$ $$\ce{(AB) ->[k_3] B + B}$$
Supposing these are "elementary" reactions, then,
$$\frac{d}{dt}(AB) = k_1[A][B] - k_2 (AB) - k_3[B]$$
If we apply the pseudo-steady state hypothesis to (AB):
$$\frac{d}{dt}(AB) = k_1[A][B] - k_2 (AB) - k_3[B] = 0$$ $$(AB) = \frac{k_1[A][B] - k_3[B]}{k_2}$$
We can additionally eliminate [A] from this equation because by stoichiometry, $[A] + (AB) + [B] = C$, where C is a constant. For simplicity, let's also suppose that (AB) will always be very low compared to [A] and/or [B]. But if (AB) is always low, we can approximate this by $[A] + [B] = C$. If so, then $[A] = C - [B]$. Substituting this into the equation above:
$$(AB) = \frac{k_1\left(C - [B] \right)[B] - k_3[B]}{k_2}$$ $$(AB) = [B]\frac{k_1\left(C - [B] \right) - k_3}{k_2}$$
Now, the rate of formation of [B] is what we are interested in. The 2nd reaction gives us the rate:
$$\frac{d}{dt}[B] = 2 k_3 (AB)$$
We can sub in the equation for (AB) we got above:
$$\frac{d}{dt}[B] = 2 k_3 [B]\frac{k_1\left(C - [B] \right) - k_3}{k_2}$$ $$\frac{d}{dt}[B] = 2 \frac{k_3}{k_2} \left([B]k_1\left(C - [B] \right) - k_3[B]\right)$$ $$\frac{d}{dt}[B] = r_B = 2 \frac{k_3}{k_2} \left( \left(k_1 C -k_3\right)[B] - k_1 [B]^2 \right)$$ $$\frac{d}{dt}[B] = r_B = 2 \frac{k_3 k_1}{k_2} \left(- [B]^2 + \left(C - \frac{k_3}{k_1}\right)[B] \right)$$
That factor in parenthesis is a quadratic in [B]. We can find when the rate will be a maximum by differentiating this term with respect to [B] and setting the result to zero.
$$-2 [B]_{maxrate} + (C - \frac{k_3}{k_1}) = 0$$ $$[B]_{maxrate} = \frac{1}{2}(C - \frac{k_3}{k_1})$$
This shows that the rate of formation of [B] will have a maximum. (Well technically an extremum but if you take the 2nd derivative you will find the extremum we found is in fact a maximum.)
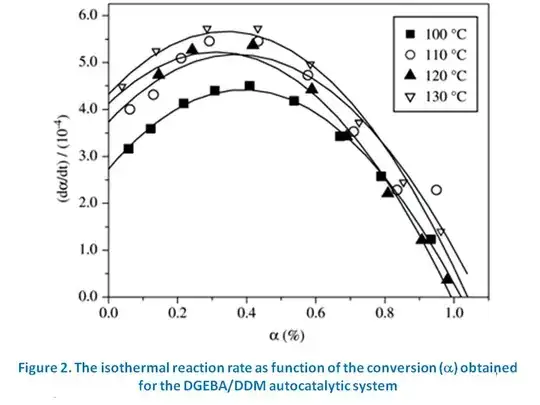
You indicated in your question that the curves you drew represented plots not of concentration, but of the reaction rate. The only curve that has a maximum rate is curve B, therefore it must be the right answer.
