Sequential first order reaction graph in chemical kinetics

Question

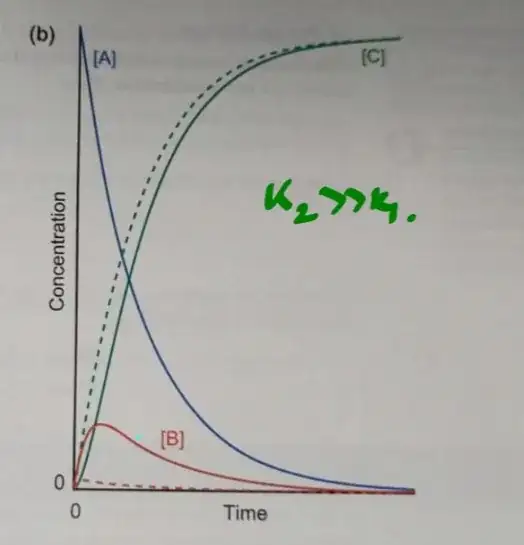
In graph given below is a sequential first order reaction

$$\ce{A ->[$k_1$] B ->[$k_2$] C}$$

For $k_2 \gg k_1$ the graph of concentration of $\ce{A}$, $\ce{B}$ and $\ce{C}$ is as follows.

Won't the graph of the concentrations of $\ce{B}$ and $\ce{C}$ be the same as if $\ce{B}$ is formed then only $\ce{C}$ will be formed simultaneously? Then why is $\ce{C}$'s graph different?

The answer to your doubt is directly on your graph. First some B has to be created. Initially, the rate of C formation is zero. — Poutnik, Jun 24 '23 at 16:06
My doubt is if B is only not formed then will C form? Then why the graph of concentration is different? — A 10th grader, Jun 24 '23 at 17:00
Neither of questions is clear. Try to reformulate. // C is formed only from B. If no B is present, no C is being formed. — Poutnik, Jun 24 '23 at 17:07
The concentration profiles of B and C are not the same because B is formed only from A and then B only forms C so the concentration of B rises and falls but C only rises as it does not react to form anything else. — porphyrin, Jun 25 '23 at 12:21
Are the two reactions elementary? Can one assume mass action kinetics? — Rodrigo de Azevedo, Jun 27 '23 at 07:24
See also Pre-equilibrium approximation for k1 >> k2 and Steady State Approximation for k1 << k2. — Poutnik, Jun 27 '23 at 07:36
https://chemistry.stackexchange.com/questions/40785/meaning-of-steady-state-kinetics/40796#40796 — Curt F., Jun 28 '23 at 01:12

score 1 · Answer 1 · edited Jun 26 '23 at 18:43

This question is about the rate-determining step of multi-step reactions. Bear in mind that the overall rate of reaction is equal to the slowest step of the reaction, in which case, from $\ce{A}$ to $\ce{B}$ ($k_2 \gg k_1$). Since it is a first-order reaction, the overall reaction rate = $k_1 [\ce{A}]$. The graph of concentration vs time for a first-order reaction should be like $y = \frac1x$.

On the other hand, $\ce{B}$ is the reaction intermediate. $[\ce{B}]$ initially increases when the reactant $\ce{A}$ is gradually consumed. But soon, $[\ce{B}]$ reduces to form $\ce{C}$.

The graph of $[\ce{C}]$ must be symmetrical about the horizontal line $y = \frac12[\ce{A}]$ because as stated earlier, the overall reaction rate $= k_1 [\ce{A}]$.

ananta · Answer 2 · 2023-06-27T08:20:18.660

1

This is a pseudo first-order reaction. The rate of product formation is:

$$ \mathrm{R} = \dfrac{\mathrm{d}}{\mathrm{d}t}\ce{[C]}= k_2\ce{[B]} \tag{1}\\ $$

Applying steady state approximation:

$$ \dfrac{\mathrm{d}}{\mathrm{d}t}\ce{[B]}= k_1\ce{[A]} - k_2\ce{[B]} \approx 0 \tag{2} $$

$$ \implies k_1\ce{[A]} \approx k_2\ce{[B]}\\ \implies k_1\ce{[A]} \approx k_2\ce{[B]} $$

Substituting in Equation (1):

$$ R \approx k_1\ce{[A]} $$

For the overall reaction $\ce{A -> C}$:

$$ -\dfrac{\mathrm{d}}{\mathrm{d}t}\ce{[A]} = k_1\ce{[A]}\\ \implies \ce{[A]} = \ce{[A]_o}\mathrm{e}^{-k_1t} \tag{3} $$

edited Jun 27 '23 at 08:20

answered Jun 27 '23 at 07:49

ananta

2,289
3
22

Are you assuming mass action kinetics? – Rodrigo de Azevedo Jun 27 '23 at 08:06
@RodrigodeAzevedo it is applicable for low concentrations. – ananta Jun 27 '23 at 08:11
Do you mean (1) is applicable? – Rodrigo de Azevedo Jun 27 '23 at 08:12
@RodrigodeAzevedo (1), (2), and (3). – ananta Jun 27 '23 at 08:14

Sequential first order reaction graph in chemical kinetics

2 Answers2