Change in Gibb's free energy at equilirbrium

Question

I know the basic relation that ΔG=ΔG⁰+RTln(Q) where Q is the reaction quotient, my doubt is that if Q=1 at equilibrium then ΔG=ΔG⁰ but will ΔG=0 or ΔG≠0? As far as I know, generally at equilibrium Q=Keq, ΔG=0.

Answer 1

As $$\Delta_r G^{\circ}=-RT \ln K$$

then

$$\Delta_r G=\Delta_r G^{\circ} + RT \ln Q = RT \ln{\frac{Q}{K}}$$

If there is by the task conditions equilibrium and $Q=1$ then

\begin{align} K&=1\\ RT \ln K &= 0\\ RT \ln Q &= 0\\ \Delta_r G^{\circ}&=0\\ \Delta_r G&=0 \end{align}

Answer 2

Note:At equilibrium ∆rG is always zero And at Q=1,∆rG is always equal to ∆rG°

Both are different concepts and you are merging them into one. Let's understand them one by one.

First of all , the equation you have written is not correct , there must be ∆rG instead of ∆G. Both are different . ∆G is difference of Gibbs free energy between any two states of system whereas ∆rG is derivative of Gibbs free energy with respect to extend of reaction. Now understand difference between these two terms in more detail.

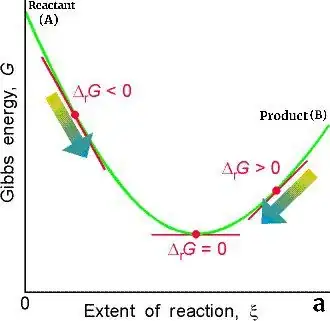
Let's consider a reaction A -> B and plot the graph of Gibbs free energy vs extent of reaction for this reaction.

a = initial mole of reactant A

Extent of reaction ξ means amount of reactant converted into product like ξ = 0 , no amount of reactant is converted into product hence ξ = 0 represent pure reactant. Similarly ξ = a means all reactant is converted in product , no reactant is left over so ξ = a means pure product.

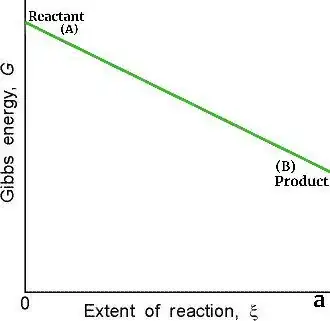
Although you might be wonder that this graph should be like that-

Yes , this graph of straight line is correct but only when there is no mixing between reactant and product. Mixing involves interaction phenomenon between reactant and product molecules and due to this at Gibbs free energy is lower than expected and correct graph is that curved one.

If you want to further read about mixing - check out these links

Lecture on Gibbs free energy of mixing

Article on Thermodynamics of mixing

Okay so let's get back to our reaction where mixing is involved -

∆G is difference of Gibbs free energy between any two points , if we take X and Y two points then ∆Gxy will represent Gibbs free energy difference between these two points.

∆rG- iIf at any point a infinitesimal amount dξ of reactant A is converted into B and difference in Gibbs free energy due to this small change is dG then ∆rG is dG/dξ.

If still you are confused with ∆G and ∆rG read this answer - https://chemistry.stackexchange.com/a/50585/129242

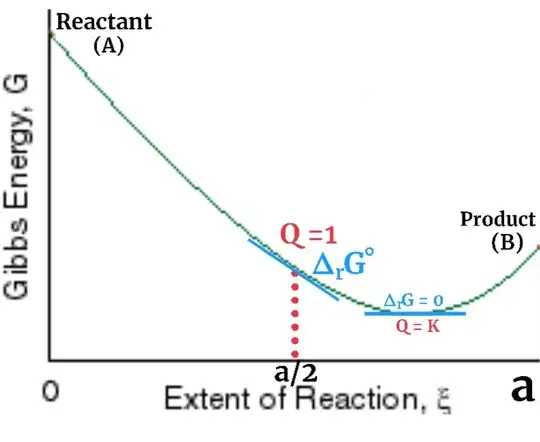
∆rG°

As we take electrode potential of hydrogen zero as reference for convince because we can't measure it in absolute terms similarly we take ∆rG° (or Q = 1) as reference for a reaction so that we can further calculate variation of ∆rG with the concentration of reactant and product using the formula ∆rG = ∆rG° + RTln(Q). ∆rG° simply denotes ∆rG at a specific point when reaction quotient (Q) = 1. ∆rG° has nothing to do with equilibrium.

In this example if we consider reaction elementary then reaction quotient cna be written as Q = [B] / [A] where [•] represent concentration. Also we assume that solution in which reaction is going on has volume 1 litre so concentration = moles.

So reaction quotient will be equal to one Q = 1 when [A] = [B] or ξ = a/2.

Equilibrium

Same like ∆rG° which denotes a special point in terms of reaction quotient where Q = 1, equilibrium ( at which Gibbs free energy of system is minimum) is special point (here Y) in terms of Gibbs free energy at which ∆rG = 0 , Equilibrium doesn't have any specific value of Q , at equilibrium Q may be equal to one or may not be. Also remember that Q at equilibrium is known as Equilibrium constant Keq.

In this diagram you can clearly see that Q = 1 , where ∆rG = ∆rG° and Q = Keq , where ∆rG = 0 are two different points.

Finally discuss your question.

---

I know the basic relation that ΔG=ΔG⁰+RTln(Q) where Q is the reaction quotient, my doubt is that if Q=1 at equilibrium then ΔG=ΔG⁰ but will ΔG=0 or ΔG≠0? As far as I know, generally at equilibrium Q=Keq, ΔG=0.

---

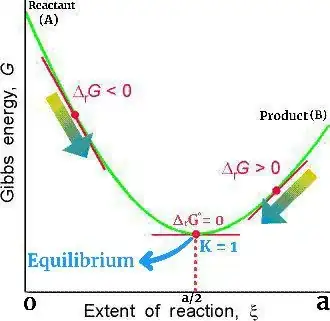
Question is about a special case where Q = 1 at equilibrium . When Q = 1, ∆rG = ∆rG° and at equilibrium ∆rG = 0 so final conclusion is that in this case ∆rG° will also be equal to 0.

So in our reaction A -> B whose thermodynamics and Equilibrium we have already discussed, if Q = 1 at equilibrium then Gibbs free energy diagram will look like -

Comment if any point is not clear to you.