Do symmetric hydrogen bonds in neutral molecules exist?

Question

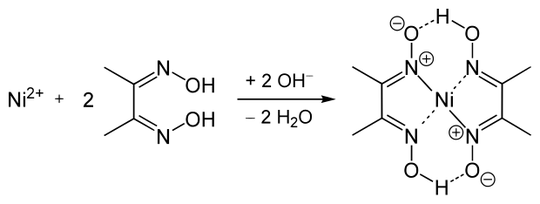
As far as I know, there have only few truly symmetric hydrogen bonds been observed. Unquestionable is the existence of it in the bifluoride ion, $\ce{[F-H-F]-}$, see also here. There are a couple of more, like in a water hydroxyl complex $\ce{[HO\bond{~}H2O]- @Cu($110$)}$,^[1] or in the hydrogen disuperoxide anion $\ce{[O2-H-O2]-}$.^[2]

Long time it was believed that malonaldehyde and acetylacetone^[3] form keto-enol tautomers with symmetric hydrogen bonds. The reason for this is the lack of resolution of the experiments.

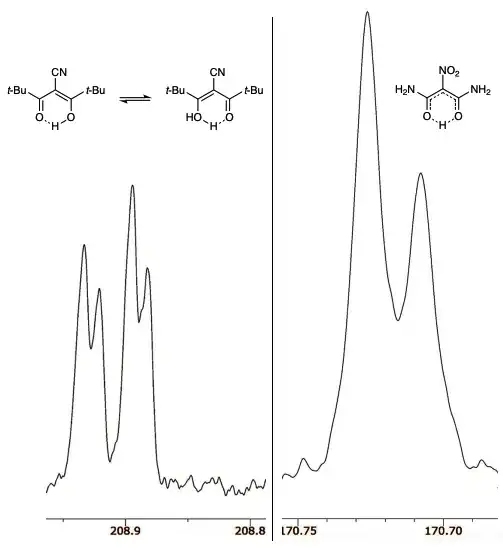
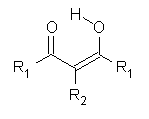
I recently came across the article about substituted malonaldehydes.^[4] According to this, if you chose R1 to be an amine and R2 a nitro group, you could end up with a single well on the potential energy surface.

However, there is one response, that left me a bit puzzled. Henry Rzepa wrote:

Searches of the Cambridge crystal structure database will reveal quite a number of instances of symmetrical hydrogen bonds. These are mostly homonuclear, ie N…H…N or O…H…O. Years ago, we came across a more unusual example, of an (almost) symmetrical N….H….O heteronuclear example (http://dx.doi.org/10.1039/C39890001722 ).

So apparently there exist many. Unfortunately, he doesn't extend us the courtesy of even a single example. If you look on Google Scholar, you do indeed find a few examples of symmetric hydrogen bonds. However, most of them are either "crystallograpically" symmetric, for charged species, or both.

Also Evangelista et al. conclude their paper about malonaldehydes with the following statement, which leads me to believe, that there is no such thing as a symmetrical hydrogen bond in a neutral molecule:

A remaining goal is the identification of a substituted malonaldehyde with no barrier at all, i.e., a C_2v equilibrium geometry.

Since then a few more years have passed, but my search did not turn up any more results.
Do symmetric hydrogen bonds in neutral molecules exist?

What about diborane? Does that even count as hydrogen bonding? — SendersReagent, Mar 03 '16 at 08:43
@DGS This is actually quite an interesting stand. I did not think about that. I really need to wrap my head around that and maybe make a few searches if anyone has ever called it a hydrogen bond. — Martin - マーチン, Mar 03 '16 at 08:50
The big difference there is that normal hydrogen bonds are 4-electron, 3-atoms. In the case of diborane, they are 2-electron, 3-atom bonds. Could almost call them hydride bonds instead of hydrogen bonds. — SendersReagent, Mar 03 '16 at 09:01
@DGS Yes that's correct. They are also the prime example for 3c2e-bonding, covalent through and through. For the sake of the question, it is probably better to exclude them. — Martin - マーチン, Mar 03 '16 at 09:06
@SendersReagent IUPAC defined hydrogen bond as "an attractive interaction between a hydrogen atom from a molecule or a molecular fragment X–H in which X is more electronegative than H..." http://www.currentscience.ac.in/Volumes/110/04/0495.pdf So because boron is less electronegative than hydrogen, diborane does not involve hydrogen bonds. — DavePhD, Apr 11 '16 at 18:14
@DavePhD That's what I figured. On the topic, anyone ever seen anything on a protonated proton sponge salt? Maybe symmetrical? — SendersReagent, Apr 11 '16 at 18:41
I think this is a great question but most answers attempt to find examples to prove that there are such cases, rather than exploring what conditions must be satisfied, and why it may be impossible to do so. I suspect the answer might be "no" for theoretical reasons: first, the acceptor/donor heavy atoms have to be placed in the right geometry to be equidistant from the well minimum. That is hard enough, but the many examples show it's (probably) not inherently impossible. Second, if you find an optimal geometry, then "orbitals from the two heavy atoms overlap" at the site of the proton. — Buck Thorn, May 23 '19 at 14:37
I use quotation marks because it's the MOs you need to think about. What I wonder is if exclusion principle might not lead to the impossibility of such sharing, ie the orbitals involved are antisymmetric leading to a node. Out on a limb waving my arms feeding thoughts. — Buck Thorn, May 23 '19 at 14:41
Perhaps you should add modify your question to "have symmetric hydrogen bonds in neutral molecules been reported? If not, are they possible?" Despite being interesting, as it stands the question is flawed because it is too broad: it is impossible to sample the realm of all molecules. — Buck Thorn, May 26 '19 at 19:57
Here’s a recent paper arguing that the hydrogen bond in phthalates is inherently asymmetric (i.e. an equilibrium): https://doi.org/10.1021/jacs.9b08492 — orthocresol, Oct 19 '19 at 15:21

Mithoron · Answer 1 · 2024-02-10T15:22:43.127

It appears that, perhaps, water may have symmetric hydrogen bonds between oxygen atoms, but it would take at least 60 GPa of pressure, to make water to bond like that. I guess water stops being molecular, because of that, though.

Article named very descriptively "Compression of Ice to 210 gigapascals: Infrared Evidence for a Symmetric Hydrogen-Bonded Phase" implies that:

Protonated and deuterated ices ($\ce{H2O}$ and $\ce{D2O}$) compressed to a maximum pressure of 210 gigapascals at 85 to 300 kelvin exhibit a phase transition at 60 gigapascals in $\ce{H2O}$ ice (70 gigapascals in $\ce{D2O}$ ice) on the basis of their infrared reflectance spectra determined with synchrotron radiation. The transition is characterized by soft-mode behavior of the $\nu_3$ $\ce{O-H}$ or $\ce{O-D}$ stretch below the transition, followed by a hardening (positive pressure shift) above it. This behavior is interpreted as the transformation of ice phase VII to a structure with symmetric hydrogen bonds.

On the other hand, article "The Hydrogen Bond in the Solid State" mentions:

First example of an $\ce{O-H-N}$ hydrogen bond with a centered position of the proton: pentachlorophenol/4-methylpyridine at 100 K characterized by neutron diffraction studies (...)

Unfortunately:

Even very small chemical changes in the system lead to loss of the symmetry (...)

so symmetric hydrogen bonds can probably exist also in very low temperatures.

References

Goncharov, A F; Struzhkin, V V; Somayazulu, M S; Hemley, R J; Mao, H K. Science 273.5272

Steiner, Thomas Angew. Chem. Int. Ed. 41 1 71

This is certainly an interesting and unexpected take on the matter. I admit I was not hoping for something like this. Thanks for digging it up. — Martin - マーチン, Apr 22 '16 at 06:20
I think I read sth similar about carboxylic acid dimers (also pressure symmetrization). I think it's quite possible also in normal pressure in certain situations, maybe I'll find more... — Mithoron, Apr 23 '16 at 01:38
@Mithoron I have been reading a bit about ice and I came across this paper (Benoit, M., Marx, D., & Parrinello, M. (1998). Nature, 392(6673), 258.) which uses DFT/PIMD trying to simulate the transition to ice X (the phase described in the paper you link). They note that this phase actually does not have a single well, but still has a double well with the proton symmetrically delocalized across both wells via zero point energy. They do find a transition to a single well at even higher pressure, but from what I can tell this has not been found experimentally. — jheindel, Jul 02 '19 at 19:04

score 18 · Answer 2 · edited May 25 '23 at 14:38

This question crossed my mind during a lab today because we were making $\ce{Ni(dmg)2}$, which is shown below.

Ni(dmg)2

Well first, this is charged in some sense, but it is net-neutral. Also, the configuration shown above is only one way to draw it, and it seems as if everything should be symmetrical and thus that hydrogen should be equally shared between the two oxygens which I believe ought to be classified as a symmetric hydrogen bond on the basis of the fact there must be 4 electrons present here where that hydrogen could be equally shared. As opposed to something like diborane which was being discussed in the comments and is better classified as a 3-centre 2-electron bond.

Indeed, I dug around and found this paper which is quite old but also very interesting! They measure the infrared spectrum of this compound and a related copper compound and find a peak at about $2322\ \mathrm{cm^{-1}}$ which is an absurd shift in frequency from a normal $\ce{O-H}$ vibration. They verify this by forming the deuterated version and finding a large frequency shift down.

They say themselves, "the infrared data interpreted in terms of the abnormal isotope effect indicate that solid $\ce{Ni(dmg)2}$ and $\ce{Ni(emg)2}$ have symmetrical $\ce{OHO}$ and $\ce{ODO}$ bonds."

So then what is this "abnormal isotope effect"? Well, they also studied $\ce{Cu(dmg)2}$ and measured the $\ce{OH}$ and $\ce{OD}$ frequencies. They measured $2382\ \mathrm{cm^{-1}}$ and $2370\ \mathrm{cm^{-1}}$ respectively. Yes, a shift of $12\ \mathrm{cm^{-1}}$ upon deuteration. This effect had apparently been observed before, and the interpretation is that when the hydrogen is present, the hydrogen bond there is symmetrical, but when the oxygen is deuterated, the deuterium bonds more strongly to the oxygen (for some unknown reason to me) and thus is shared unequally which raises the frequency (despite the lowering due to a larger reduced mass).

So not sure if that's exactly what you're looking for, but I thought it close enough to your description to post here.

Obviously what remains to be seen is whether or not this actually corresponds to a single well on the potential energy surface. I would guess that it does simply because of the symmetry present in the system along with the evidence presented above.

EDIT:

Thanks to Martin for running a calculation to see whether or not there is really a single well, and despite some good experimental evidence, he found the hydrogen bond to be asymmetric.

This paper also indicates the same. So alas we haven't found an answer yet.

References:

Caton Jr, J. E., & Banks, C. V. (1967). Inorganic Chemistry, 6(9), 1670-1675.

Bruce-Smith, I. F., Zakharov, B. A., Stare, J., Boldyreva, E. V., & Pulham, C. R. (2014). The Journal of Physical Chemistry C, 118(42), 24705-24713.

This is very interesting indeed. I will run a calculation on it to check for the single well. It could be a similar case to malonaldehyde/acetylacetone, where it appears to be symmetric at first glance only. For now, have my upvote. — Martin - マーチン, Oct 20 '16 at 06:38
I've done a really quick calculation (DF-BP86/def2SVP) and found that the complex in the equilibrium geometry has only $C_\mathrm{2h}$ symmetry. The bond lengths are $\mathbf{d}(\ce{O-H})=110.2~\mathrm{pm}$ and $\mathbf{d}(\ce{O\bond{~}H})=137.0~\mathrm{pm}$. After that I found a paper, that confirms my result: Ian F. Bruce-Smith et. al, J. Phys. Chem. C 2014, 118 (42), 24705–24713. In conclusion: unfortunately not a single well, not a symmetric hydrogen bond. — Martin - マーチン, Oct 20 '16 at 10:06
Ah bummer. I guess it's never completely safe to trust a paper from 1967 cause they obviously couldn't run the calculations we can. Nonetheless, it's a pretty interesting interaction! — jheindel, Oct 20 '16 at 18:25
Not trust is maybe too strong. I think the papers published at the time are trustworthy. You just have to factor in development of analysis tools, increased resolution of experiments, etc. Nevertheless, prior to your post I did not think about organometallics to achieve symmetric hydrogen bonds; while not the answer I was hoping for, it provides an interesting new direction. I would like to encourage you to include the reference I found in your last paragraph, just to make it clear. Not all people read the comments. In any case, thank your very much for your effort. — Martin - マーチン, Oct 21 '16 at 05:42
Couldn’t the discrepancy between $\ce{O-H\bond{...}O}$ and $\ce{O-D\bond{...}O}$ be explained by tunneling? Deuterium, being twice as heavy as protium has a reduced probability of tunneling, which could macroscopicly be interpreted as ‘sticking’ to one side more. (CC@Mart) — Jan, Oct 22 '16 at 00:55
@Jan So then are you saying that the protium tunnels back and forth between oxygens which macroscopically makes the hydrogen bond appear to be symmetric? — jheindel, Oct 22 '16 at 03:52
Protium is lighter. Lighter things have a greater tunneling probability, and more broadly lighter things deviate more from prequantum "classical mechanics". — Oscar Lanzi, May 25 '23 at 16:31

orthocresol · Answer 3 · 2019-05-08T22:11:07.637

In Schaefer's paper,^[1] which you linked, the authors describe nitromalonamide as being the compound with the lowest calculated barrier to intramolecular proton transfer, or tautomerisation.

Earlier this month (Feb 2019), Perrins and Wu used NMR isotope shifts to show that nitromalonamide possesses a symmetric hydrogen bond.^[2] This is "the first case, to be compared with the FHF⁻ anion, of a neutral species with a single symmetric structure in solution and with a centred hydrogen".

The authors showed this by synthesising a mixture of oxygen-18 isotopologues. It's easier to explain this starting with an example of a hydrogen bond that is not symmetrical, such as 4-cyano-2,2,6,6-tetramethylheptane-3,5-dione, which the authors used. Consider the three possible isotopologues:

For the ¹⁶O₂ isotopologue, because the equilibrium constant $K$ is equal to $1$, both C–3 (indicated by a solid arrow) and C–5 (dashed arrow) have the same chemical shift (they interconvert between a "keto" carbon and an "enol" carbon, but because they spend equal amounts of time in both tautomeric forms, the averaged shift for both carbons is the same).
The same can be said about the ¹⁸O₂ isotopologue. However, although both carbons here (brown arrows) have the same chemical shift as each other, they do not have the same chemical shift as the carbons in the ¹⁶O₂ isotopologue (blue arrows). This is because the adjacent ¹⁸O leads to a slight isotope shift.
For the ¹⁶O¹⁸O isotopologue, one might naively think that the purple carbon (C–3) should have the same chemical shift as the brown carbons in the ¹⁸O₂ isotopologue. This would be true if this equilibrium constant were equal to $1$. However, by virtue of introducing unsymmetrical isotope labelling, the equilibrium constant is no longer $1$; more specifically, it favours the C–¹⁸OH tautomer, which has a lower vibrational zero-point energy. Therefore, in this isotopologue, the purple and green carbons differ from each other in chemical shift, and also differ from the shifts in the previous two isotopologues, for a total of four peaks.

On the other hand, in nitromalonamide, which has a symmetrical double bond and therefore does not exist in an equilibrium of two tautomers, we have a different situation:

For the ¹⁶O₂ isotopologue, both blue carbons are equivalent by symmetry and hence exhibit the same shift.
For the ¹⁸O₂ isotopologue, both brown carbons are equivalent and hence have the same shift as each other, but differ from the shift in the ¹⁶O₂ isotopologue because of the aforementioned isotope shift.
In the ¹⁶O¹⁸O isotopologue, now, because there is no equilibrium to speak of, C–3 (brown arrow) has the same chemical shift as the two carbons in the ¹⁸O₂ isotopologue.^[3] So, we end up with only two peaks.

This is, of course, what is seen in the NMR spectra (of all three isotopologues together):

Notes and references

Hargis, J. C.; Evangelista, F. A.; Ingels, J. B.; Schaefer, H. F. Short Intramolecular Hydrogen Bonds: Derivatives of Malonaldehyde with Symmetrical Substituents. J. Am. Chem. Soc. 2008, 130 (51), 17471–17478 DOI: 10.1021/ja8060672.
Perrin, C. L.; Wu, Y. Symmetry of Hydrogen Bonds in Two Enols in Solution. J. Am. Chem. Soc. ASAP DOI: 10.1021/jacs.8b13785.
Theoretically, there should be a three-bond isotope shift arising from the remote oxygen being of a different isotope. However, I suspect that this effect is too tiny to be measured. Three-bond isotope shifts are known, especially with H/D, but a cursory search of the Internet didn't reveal anything about ¹⁶O/¹⁸O.

It seems like we should clarify if by a symmetric hydrogen bond, we mean a hydrogen bond where the proton exists in a single symmetric well with the minimum halfway between two groups, or if we mean any symmetrically distributed proton. In reading this paper, it seems to me that they cannot distinguish whether this is a single or double well because if the barrier is as small as some of the theory suggests, the proton could be evenly shared by having a relatively large zero point energy, which I think would result in the same NMR results. I wonder if this makes sense and what you think? — jheindel, May 22 '19 at 00:10
I find this very interesting and enlightening, but I still have doubts. On the NMR (what did they actually measure btw) timescale it appears as symmetrical, but most calculations show a double well with a tiny barrier (small enough that you may pick a DFA and receive varying results). So while this is probably as close as we get so far, it is not really what I was looking for. — Martin - マーチン, May 22 '19 at 09:23
@jheindel My interpretation of the paper is as follows: if the potential was a double well, then for the 16O/18O mixed isotopomer the two minima (or the two lowest vibrational states) would have different energies, which would result in different shifts for the 16O-bound carbon and the 18O-bound carbon. This doesn’t matter if the interconversion on the NMR time scale is fast or slow (it is most definitely fast), because the Boltzmann-averaged shifts for those two carbons (which is the relevant quantity for fast equilibria) will still be different (as illustrated by the cyano compound). — orthocresol, May 22 '19 at 09:59
On the other hand, if it’s a single well, then there cannot be any such asymmetry, as there is just one minimum. In principle, a perfectly symmetrical double well cannot be differentiated from a single well, which is (I think) your line of questioning (forgive me if I misinterpret). That is true for the 16O/16O and 18O/18O isotopomers, where you only see one peak regardless of double/single well, but the authors rely on the fact that the asymmetry in a double well for the 16O/18O isotopomer is detectable via chemical shifts. @Martin-マーチン (sorry, comment ping limitations; and it was 13C NMR). — orthocresol, May 22 '19 at 10:03
I’m not totally sure about the case where the barrier is so shallow that the zero-point energy of the molecule is larger than the barrier. That’s somewhat pathological and I’m not sure if you can measure such a thing experimentally at all, since you can’t actually detect molecules without zero-point energy to probe the shape of the PES underneath that (maybe you can, but certainly not within what I know). Then I suppose the only recourse is to computational methods. — orthocresol, May 22 '19 at 10:13
What kind of experimental technique would be able to achieve a resolution that rules out the possibility of any sort of underlying double well existing? — Blaise, May 22 '19 at 10:43
@orthocresol thanks for the explanation from an NMR perspective. I normally think about vibrational problems so this is a bit different for me. It does seem like if there is a double well, this is a case where the ZPE along that proton transfer mode exceeds the height of the barrier by about a factor of 10 based on the numbers from calculations and an estimate of the frequency of this vibration. — jheindel, May 22 '19 at 18:20
There are cases when a double well actually changes to a single well dependent on the level of theory though. Most notably in the case of $\ce{H5O2+}$. Perhaps better calculations are needed in this system to corroborate the existence of a single well. Perhaps I will try. — jheindel, May 22 '19 at 18:22
@jheindel They use a more than solid level of theory in [1]. Next level would probably be full-CI optimisations at the complete basis set limit. Have fun with that, we'll talk again in a year ;P. Also, this is a case where (IIRC) BP86 would predict a single well. I'm not sure whether any experimental technique can resolve single vs. double well, but this is interesting and certainly a mind-twister. And if we indeed observe the symmetric hydrogen bond, why are these elaborate methods failing? (cc ortho, obviously) — Martin - マーチン, May 23 '19 at 15:42

score 3 · Answer 4 · edited May 23 '19 at 00:40

I believe the anhydrous Hydrogen Fluoride ring (HF)₆ would be an example. I'm not certain, and can't find proof in literature, but it definitely looks the part!

(image was drawn myself)

As we would expect it releases heat when forming from HF, and the reaction 6HF -> (HF)₆ has an enthalpy of $\pu{-167kJ/mol}$ according to an experiment by Franck and Meyer as referenced in Fluorine Chemistry, Volume 5 . This is on the order of what we might expect from 6 Hydrogen bonds. The moiety is stable at STP while in an HF atmosphere with a very neutral Gibbs of formation from HF of $\pu{-0.8kJ/mol}$, according to thermodynamics data taken from JANAF for HF and (HF)₆. This said, these tables may have some issues, as we're exploring in another question.

In the gas phase, Hydrogen Fluoride also forms dimers, trimers, tetramers, and chains, but I think the example of the ring is easiest to see as an actual neutral bond, and not something akin a Zwitterion.

I'm still hunting for better references on this, but I did find a bulletin quoting a 1921 paper by Langmuir, of all people, saying:

"In double molecules such as H4O2 (in ice), H2F2, and in compounds such as KHF2, etc., it seems that the hydrogen nuclei instead of forming duplets with electrons in the same atom, form duplets in which the two electrons are in different atoms. The hydrogen nucleus itself thus acts like a bond in such a case. Latimer and Rodebush have made a somewhat similar suggestion in regard to hydrogen nuclei acting as bonds. They consider that the hydrogen nucleus acts on two pairs of electrons: one pair in each of the two atoms... Since the first layer of electrons in all atoms contains only two electrons, it seems probable that the hydrogen in this case also holds only two electrons and that these form the definite stable group which we have termed the duplet."

This sounds very akin to what we're hunting for, but interpreting the spectroscopic data would be unfortunately beyond my skill level. The latest and greatest the 1970s had to offer on the topic are listed in this reference on Fluorine compounds by JANAF with (HF)₆ on page 152 (1202 as listed), where they provide several references for the spectral lines. Thanks to anyone willing to give it a peak, or who may happen to know better on the topic.

This is an interesting approach to the question, and certainly has the potential to contain symmetric hydrogen bonds, as of the nature of the biflouride ion, but that brings us back to being ionic, or having large ionic contributions. I am concerned with the auto-protolysis equilibrium, $\ce{2HF <=> H+ + HF2-}$. I also ran a quick calculation on the system, it appears that a twelve-membered ring is a saddle point. While the idea remains interesting, I'm afraid it appears to not head in the right direction. — Martin - マーチン, May 23 '19 at 13:37
Thank you very much for giving it a look! If I'm understanding your point about the Bifluoride ion, it's that the system may be behaving partially as a salt of (HF2)- bound to H+? Electrostatically, I'd be surprised by the stable ring shape as compared to a more compact form. There's also a stable trimer (HF)3, which I think couldn't be rationalized as easily in this way, as there's not an even number of Fluorines to form Bifluorides. Could be a trick of resonance, of course. Happy to go with your instinct regardless, and thanks again for looking more deeply into the idea! — Michael Irving, May 23 '19 at 17:01
Names of elements and compounds aren't capitalised. As far as your comment goes, F-H-F in pure HF is countered by solvated cation H2F+. Oligomers of HF have "normal" h-bonds, if one would have symmetric one, it would dominate all others. — Mithoron, May 25 '19 at 22:55
I'd like to learn more about these gas phase ions, especially their thermodynamics data like Gibbs energies. Do you know of anywhere I can read more? — Michael Irving, May 26 '19 at 01:53

Do symmetric hydrogen bonds in neutral molecules exist?

4 Answers4

Linked