Most activated position on para-terphenyl for EAS

Question

Para-terphenyl: it doesn't look pretty with all those math-y numbers, but those are going to come helpful in answering my question!

A question asked me to tell the expected product when this reacts with $\ce{Br2/FeBr3}$. Now, I have done such questions with all types of fancy organic molecules ranging from benzene to picric acid to parantiroanisole etc. I know that I am supposed to find the most activated position¹ for EAS. But I have never done more than one phenyl ring at once.

So, in this question, I have drawn the eight resonating structures (without charge separation) of paraterphenyl manually. Here they are:

But, as you can see, every position seems to be activated identically. Each position has their own share of electrons through a pi bond, but it ends up being completely symmetric.

So, how do I find the most activated position in this compound?

---

^{1:Clarification: By "most activated position" I mean the position with maximum electron density. For example, in aniline, those are the ortho and para positions.}

Answer 1

So, how do I find the most activated position in this compound?

Start by drawing resonance structures of the various possible intermediates (sigma complexes) formed when $\ce{Br^{+}}$ attacks the different ring positions in p-terphenyl. Whichever intermediate has the most resonance structures is likely to be the most stable (lowest energy) intermediate. The lowest energy intermediate will have the smallest activation energy and consequently be the kinetically favored product (barring steric effects).

I've drawn just a few of these resonance structures in the following diagram.

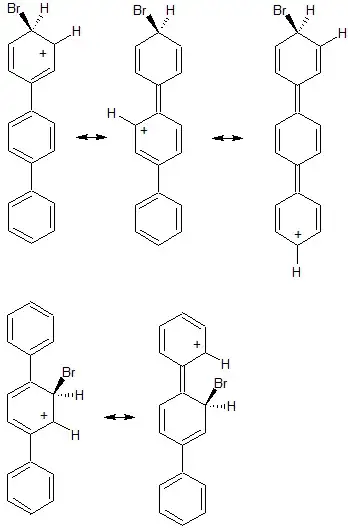
In the top row I've drawn a few of the possible resonance structures for electrophilic attack at the para position on a terminal phenyl ring. You can draw many more resonance structures delocalizing the charge around the various rings, but notice that it is possible to delocalize the positive charge over all 3 aromatic rings. In the second row I've drawn a few resonance structures showing charge delocalization when electrophilic attack occurs in the center ring. Importantly, in this case charge can only be delocalized over 2 of the aromatic rings.

This suggests that based on resonance effects, electrophilic attack on a terminal benzene ring would be preferred over attack at the central benzene ring.

Further, we would expect ortho and para attack on the terminal rings to be preferred since the phenyl substituent acts as an activating o-p director in electrophilic aromatic substitution. The rate of attack at the ortho position might also be decreased somewhat due to the steric effect of the adjacent phenyl (actually biphenyl) substituent.

In a paper by Shafig and Taylor (J. Chem. Soc., Perkin Trans. 2, 1978, 0, 1263-1267. DOI: 10.1039/P29780001263), they explore your question by studying the electrophlic protonation of tritiated p-terphenyl. After correcting the rates for statistical effects (e.g. there are twice as many ortho positions on the terminal rings as there are para positions) they find that:

• the para position (your positions $10, 16$) reacts at a relative rate of $273$
• the meta position (your positions $9, 11, 15, 17$) reacts at a relative rate of $1.54$
• the ortho position (your positions $8, 12, 14, 18$) reacts at a relative rate of $176$, and finally,
• the $4$ identical positions on the middle ring (your positions $2, 3, 5, 6$) react with a relative rate of $59.1$

These results support our predictions that

1. attack on the terminal rings will be preferred over attack on the central ring and
2. that attack at the ortho and para positions is preferred over attack at the meta position on the terminal rings.