Although the phenolate ion has more resonance structures (4) compared to acetate ion (2), acetate is more stable because it has two equivalent resonance structures of same energy.
Why does having equivalent resonance structures give more stability? Shouldn't a compound with more resonance structures be more stable?
One important thing to know is that what we call "resonance structure" is a byproduct of our chemical notation which can't describe the structure of some compounds effectively using only one chemical structure. Personally I find the old term mesomeric structure more appropriate (meso- Greek mésos in the middle; -merism from Gk. merismos "dividing, partition") because resonance is already used for a phenomena, a real phenomena, in physics that has nothing to do with resonance in chemistry. Furthermore the compound is not continuously changing it's structure between the possible resonance structures, like the term resonance seems to suggest, but is a "normal steady" compound that simply has an electron distribution that cannot be described with a single chemical structure.
The resonance energy is due to electron delocalization, so more the electrons are delocalized in the molecule higher is the resonance energy ( this means a decrease in the overall molecule energy). This is clear in the acetate ion - we can draw a resonance hybrid like this:
Here the electrons are equally distributed (delocalized) between the two oxygen atoms.
However for some compounds the real structure is not always a structure right in the middle between the different resonance structures; the first assumption is true only if the two structures are two equivalent structures. So it can occur that the electrons are not well delocalized between all the atoms hence the resonance energy is lower and so the overall stability.
In the case of phenolate ion I think the first structure in the figure [2] gives a greater contribution to the final structure of the phenolate ion so the electrons are not well delocalized, but if I'm not wrong are mainly in the oxygen atom. Unfortunately I can't find the energy of the different resonance structures.
Finally, however, I think that you should study case by case if the number of the resonance structures or their contributions are determinant to the overall resonance energy taking into account valency and electronegativity of the atoms involved.
Although the phenolate ion has more resonance structures (4) compared to acetate ion (2), acetate is more stable because it has two equivalent resonance structures of same energy.
I would argue the phenolate ion has five mesomeric structures, two with the charge assigned to oxygen (analogous to the two resonance structures of phenol), and three with the charge assigned to the ring carbon in ortho and para positions (see G M's answer).
Why does having equivalent resonance structures give more stability? Shouldn't a compound with more resonance structures be more stable?
I don't think the statement is true in this general form. It is always possible to make mesomeric structures a little bit less equivalent (for instance, through isotope-labeling of one of the oxygen atoms in acetate). This does not change the acidity of acetic acid much.
To give another example, we can compare the acidity of propene, acetaldehyde and formic acid. When you remove a proton from each of these, you get three anions that have multiple mesomeric structures.
The ones for propene and formic acid are symmetric, the one for acetaldehyde is not. Formic acid is most acidic, followed by acetaldehyde with propene least acidic. I would observe that for formate, the negative charge is assigned to oxygen for both mesomeric structures whereas for the deprotonated propene, it is assigned to a carbon atom. The enolate anion has the charge on oxygen for the more significant mesomeric structure (shown) and on carbon for the less significant one (not shown).
The argument for phenol vs acetic acid is similar. So it matters what the significant mesomeric structures are and which atom type carries the negative charge. When mesomeric structures are symmetric, it ensures that they have the same significance. If you compare apples to apples (i.e. anions where the negative charge is assigned to carbon for all mesomeric structures), it helps to distribute the charge (having the carbons with assigned charge at large distances), and having many possible locations for the charge.
For phenolate, the large number of mesomeric structures is less relevant because the ones with the charges assigned to oxygen are the most significant (the only ones that don't force us to write a structure lacking alternate double bonds in the benzene ring).
I would like to give a very rough answer as to why equivalent resonance structures have a stabilizing effect.
To begin, we assume that resonance can be represented as a discrete n-state system. Feynman has used this simple approximation to explain many of the essential features of chemical bonding and resonance in the Feynman Lectures on Physics Vol III, Chapters 8 - 10.
To simplify we begin with a molecule which can have 2 different canonical structure based on the usual rules. Let the energies of the two states be $E_1$ and $E_2$ .
The Hamiltonian of this two state system will be: $$H = \pmatrix{E_1& 0\\0&E_2}$$
The canonical structure are themselves eigen-states here. However in the real world we find more symmetry to the molecule/different bond lengths/angles than that is predicted by our canonical structures. This is because the two canonical structures are not the actual eigen states.
We assume that the new eigen states however can be represented as a superposition of the 'old' states.
Therefore in the most general case the Hamiltonian expressed in the 'old' base states become: $$H = \pmatrix{E_1 & H_{12}\\H_{12}^*&E_2}$$
We find the energy eigenvalues from this matrix.
The energy eigenvalue with the lower energy in this case is:
$$ E^{'}_1 = \frac{E_1 + E_2}{2} - \frac{\sqrt{(E_1 - E_2)^2 + 4H_{12}H_{12}^*}}{2} $$
Here without loss of generality let us assume that $E_2 \ge E_1$
So taking the difference $D = E_1 - E^{'}_1$ which is the energy difference between the old base state and the new eigenstate with lower energy: $$ D = E_1 - E^{'}_1 = \frac{E_1-E_2}{2} + \frac{\sqrt{(E_1 - E_2)^2 + 4H_{12}H_{12}^*}}{2} $$
This $D$ is a measure of the stabilization due to resonance.
Setting $E_1 - E_2 = x \le 0$, we get $$D = \frac{x}{2} + \frac{\sqrt{x^2 + 4H_{12}H_{12}^*}}{2}.$$
The graph of this function is:
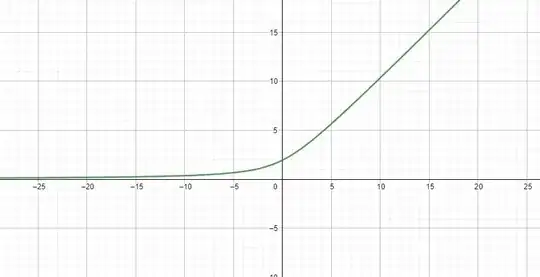
So we see that for $x \le 0$ , $D$ is maximum when $x = 0$, i.e. $E_1 = E_2$. One way this can happen is when our base states are symmetrical or in other words when the molecule has equivalent resonance structures.
However one should be careful of the comparison being made here. We are not comparing the molecule to some other molecule. All that is said here is that the stabilization of the molecule due to resonance is maximum when the canonical structures are equivalent (for a 2-state system).