How to determine the pH of a mixture of two weak acids?

Question

We have two solutions:

• Solution 1 is $\ce{HCOOH}$, its concentration is $c_1 = \pu{10^-2 mol/l}$, its volume is $V_1 = \pu{50 ml}$, and its $\mathrm{pH}_1 = 2.9$.

• Solution 2 is $\ce{CH3COOH}$, its concentration is $c_2 = \pu{10^-2 mol/l}$, its volume is $V_2 = \pu{50 ml}$, and its $\mathrm{pH}_2 = 3.4$.

How would be the equation and the ICE table, and what is the $\mathrm{pH}$ of the mixture of these two solutions?

I used numbers to differentiate the solutions, and to understand how it works, but for no other reason.

I tried to do $\mathrm{pH}=\frac{1}{2}\left(\mathrm{pH}_1+\mathrm{pH}_2\right)$, but it’s trivial and doesn't work.

Answer 1

Below a more general approach.

Suppose that we have two weak acids $\ce{HA}$ and $\ce{HB}$. The initial concentrations are $C^0_\ce{HA}$ and $C^0_\ce{HB}$, and their constants are $K_{\mathrm{a},\ce{(HA)}}$ and $K_{\mathrm{a},\ce{(HB)}}$. Suppose yet that volumes, $V_\ce{HA}$ and $V_\ce{HB}$, are additives. So we have:

1. Reactions

\begin{align} \ce{HA + H2O &<=> H3O+ + A-} & K_{\mathrm{a},(\ce{HA})} &= \frac{\ce{[H3O+][A-]}}{\ce{[HA]}} \tag{1}\label{eq:KAcidHA}\\ \ce{HB + H2O &<=> H3O+ + B-} & K_{\mathrm{a},(\ce{HB})} &=\frac{\ce{[H3O+][B-]}}{\ce{[HB]}} \tag{2}\label{eq:KAcidHB}\\ \ce{2 H2O &<=> H3O+ + OH-} & K_\mathrm{w} &= \ce{[H3O+][OH-]}\tag{3}\label{eq:KWater} \end{align}

2. Mass balance

\begin{align} C_\ce{HA} &= \frac{C^0_\ce{HA} V_\ce{HA}}{V_\ce{HA} + V_\ce{HB}} &&=\ce{[HA] + [A-]}\tag{4}\label{eq:MassBalanceHA}\\ C_\ce{HB} &= \frac{C^0_\ce{HB} V_\ce{HB}}{V_\ce{HA} + V_\ce{HB}} &&=\ce{[HB] + [B-]}\tag{5}\label{eq:MassBalanceHB} \end{align}

3. Charge balance

$$\ce{[H3O+] = [OH-] + [A-] + [B-]}\tag{6}\label{eq:ChargeBalance}$$

Replacing \eqref{eq:KAcidHA}–\eqref{eq:MassBalanceHB} equations on \eqref{eq:ChargeBalance}, we have: $$ \ce{[H3O+]} = \frac{K_\mathrm{w}}{\ce{[H3O+]}} +\frac{C_\ce{HA} K_{\mathrm{a},(\ce{HA})}}{\ce{[H3O+]} + K_{\mathrm{a},(\ce{HA})}} + \frac{C_\ce{HB} K_{\mathrm{a},(\ce{HB})}}{\ce{[H3O+]} + K_{\mathrm{a},(\ce{HB})}} \tag{7}\label{eq:GeneralEquation}$$

or as polynomial

\begin{align} \begin{split} &\ce{[H3O+]}^4\\ +&\ce{[H3O+]}^3 (K_{\mathrm{a},(\ce{HA})} + K_{\mathrm{a},(\ce{HB})})\\ +&\ce{[H3O+]}^2 \left[ K_{\mathrm{a},(\ce{HA})} K_{\mathrm{a},(\ce{HB})} - ( C_\ce{HA} K_{\mathrm{a},(\ce{HA})} + C_\ce{HB}K_{\mathrm{a},(\ce{HB})} ) - K_\mathrm{w} \right]\\ -&\ce{[H3O+]} \left[ (C_\ce{HA} + C_\ce{HB}) K_{\mathrm{a},(\ce{HA})} K_{\mathrm{a},(\ce{HB})} + K_\ce{w} (K_{\mathrm{a},(\ce{HA})} + K_{\mathrm{a},(\ce{HB})}) \right]\\ -& K_{\mathrm{a},(\ce{HA})} K_{\mathrm{a},(\ce{HB})} K_\mathrm{w}\\ =&\ 0 \end{split}\tag{8}\label{eq:GeneralPol} \end{align}

This single equation will exactly solve any equilibrium problem involving the mixture of any two monoprotic acids, in any concentration (as long as they're not much higher than about $\pu{1 mol L-1}$) and any volume. Depending of $K_\mathrm{a}$, $K_{\mathrm{a},(\ce{HB})}$, $C^0_\ce{HA}$, and $C^0_\ce{HB}$ values, we can yet obtain a simpler version^[1].

The \eqref{eq:GeneralPol} equation can simplified considering^[2] that $K_{\mathrm{a},(\ce{HA})} K_{\mathrm{a},(\ce{HB})} K_\mathrm{w} \ll \ce{[H3O+]}^4$:

\begin{align} \begin{split} &\ce{[H3O+]}^3\\ +&\ce{[H3O+]}^2 (K_{\mathrm{a},(\ce{HA})} + K_{\mathrm{a},(\ce{HB})})\\ +&\ce{[H3O+]}\left[ K_{\mathrm{a},(\ce{HA})} K_{\mathrm{a},(\ce{HB})} - (C_\ce{HA} K_{\mathrm{a},(\ce{HA})} + C_\ce{HB} K_{\mathrm{a},(\ce{HB})}) - K_\mathrm{w} \right]\\ -&\left[ (C_\ce{HA} + C_\ce{HB}) K_{\mathrm{a},(\ce{HA})} K_{\mathrm{a},(\ce{HB})} + K_\mathrm{w} (K_{\mathrm{a},(\ce{HA})} + K_{\mathrm{a},(\ce{HB})}) \right]\\ =&\ 0 \end{split}\tag{9}\label{eq:GeneralPolSimp1} \end{align}

The \eqref{eq:GeneralPolSimp1} equation can simplified considering^[2] that $K_{\mathrm{a},(\ce{HA})} K_{\mathrm{a},(\ce{HB})} \ll \ce{[H3O+]}^3$:

\begin{align} \ce{[H3O+]}^2 + \ce{[H3O+]} (K_{\mathrm{a},(\ce{HA})} + K_{\mathrm{a},(\ce{HB})}) - (C_\ce{HA} K_{\mathrm{a},(\ce{HA})} + C_\ce{HB} K_{\mathrm{a},(\ce{HB})}+K_\mathrm{w}) = 0\tag{10}\label{eq:GeneralPolSimp2} \end{align}

The \eqref{eq:GeneralPolSimp2} equation can be solved as usual.

$$\ce{[H3O+]} = \frac{ - (K_{\mathrm{a},(\ce{HA})} + K_{\mathrm{a},(\ce{HB})}) + \sqrt{ (K_{\mathrm{a},(\ce{HA})} + K_{\mathrm{a},(\ce{HB})})^2 + 4 (C_\ce{HA} K_{\mathrm{a},(\ce{HA})} + C_\ce{HB} K_{\mathrm{a},(\ce{HB})}+K_\mathrm{w})} }{2}$$

Or using the initial concentrations

$$\ce{[H3O+]} = \frac{ - (K_{\mathrm{a},(\ce{HA})} + K_{\mathrm{a},(\ce{HB})}) + \sqrt{ (K_{\mathrm{a},(\ce{HA})} + K_{\mathrm{a},(\ce{HB})})^2 + 4\left(%\displaystyle \frac{C^0_\ce{HA} V_\ce{HA} K_{\ce{a},(\ce{HA})} }{V_\ce{HA} + V_\ce{HB}} + \frac{C^0_\ce{HB} V_\ce{HB} K_{\ce{a},(\ce{HB})} }{V_\ce{HA} + V_\ce{HB}} +K_\mathrm{w}\right)} }{2}$$

Replacing $C^0_\ce{HA}=\pu{0.01 mol L-1}$, $C^0_\ce{HB}=\pu{0.01 mol L-1}$, $V_\ce{HA}=\pu{0.050 L}$ and $V_\ce{HB}=\pu{0.050 L}$, and using $\text{p}K_\ce{a}=3.75$ for formic acid and $\text{p}K_\ce{a}=4.756$ for acetic acid^[3], we have $$\ce{pH}=3.05.$$

Addendum

@MaxW made some warnings about the assumptions which simplificate ($\ref{eq:GeneralPol}$)(see comment) and ($\ref{eq:GeneralPolSimp1}$)(see comment) equations. To completeness and with the aim of show the limitations of present approach, consider the following graphics. The ($\ref{eq:GeneralPol}$), ($\ref{eq:GeneralPolSimp1}$), and ($\ref{eq:GeneralPolSimp2}$) equations were solved using $\text{p}K_{\mathrm{a},(\ce{HA})}=\text{p}K_{\mathrm{a},(\ce{HB})}$, $C^0_\ce{HA}=C^0_\ce{HB}$, and $V_\ce{HA}=V_\ce{HB}=\pu{50.0 mL}$.

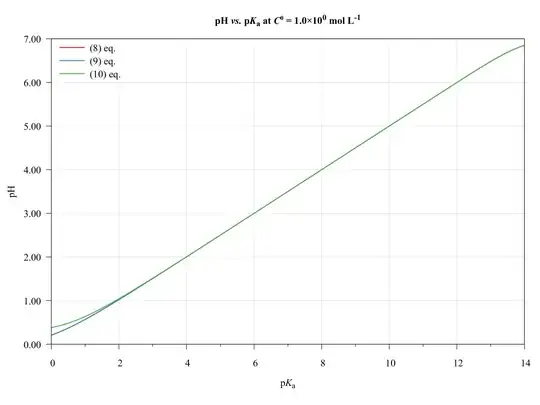
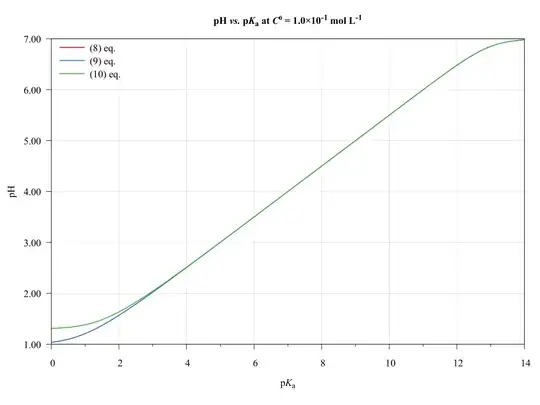
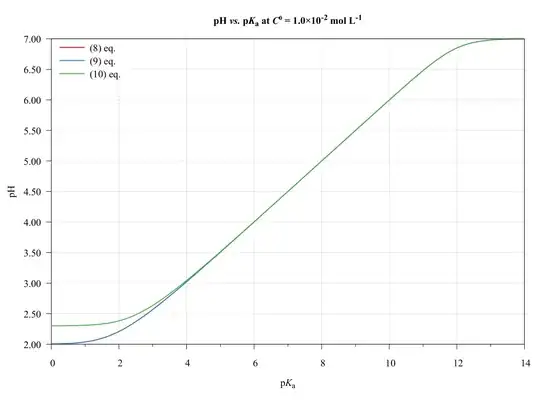
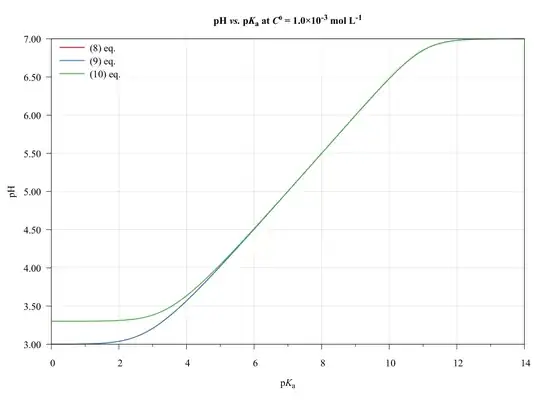
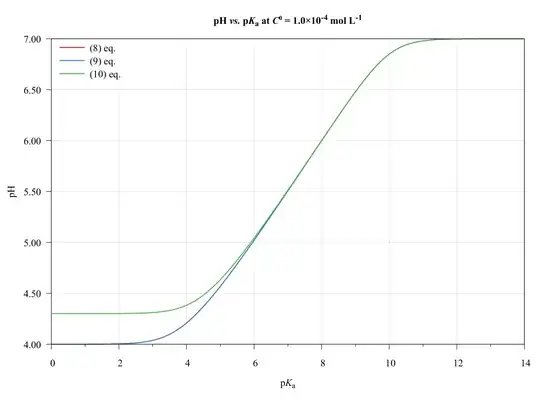
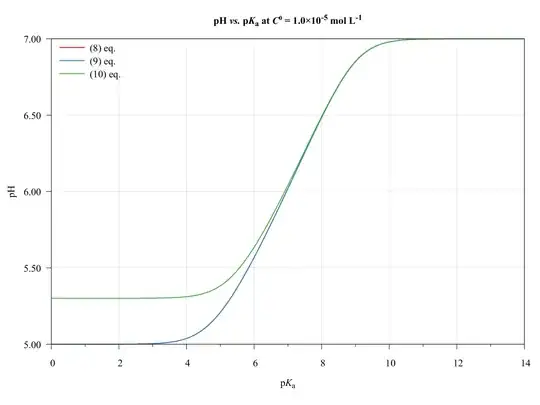
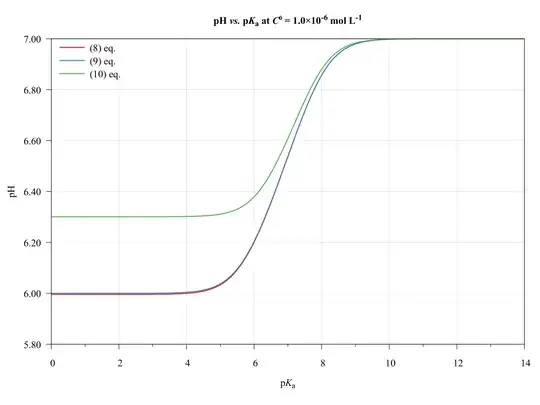
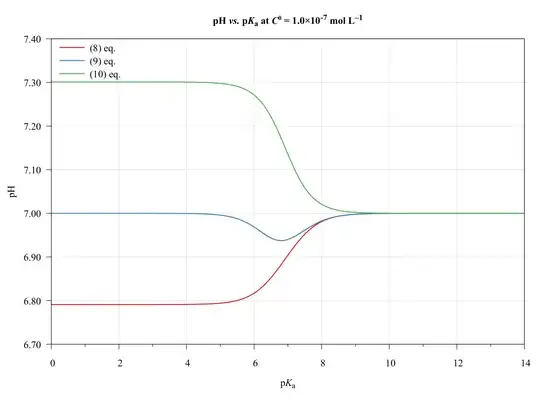
As we can see, the ($\ref{eq:GeneralPolSimp1}$) equation can be used on any $\text{p}K_\ce{a}$ values, inasmuch as the concentration be major of $\pu{1E-6 mol L-1}$. The ($\ref{eq:GeneralPolSimp2}$) equation becomes problematic when dilute solutions or strong acids solutions are used.

Thus, when applied to book-examples, which $\text{p}K_\ce{a}$ values from 3 to 6, and the concentrations from $1.0$ to $\pu{1.0E-4 mol L-1}$, the assumptions are valid and the equations can be used, providing good approximations of $\ce{pH}$ values.

Acknowledgement

Thanks to @MaxW for draw attention to limitations of assumptions.

Reference

1. Edited based on first @MaxW's comment.
2. Edited based on second @MaxW's comment.
3. Haynes, W. M.; Lide, D. R.; Bruno, T. J., CRC Handbook of Chemistry and Physics. 97 ed.; CRC Press: 2017; pp. 5–88.

Answer 2

Given the following: \begin{align} [\ce{CH3COOH}] &= \pu{1 * 10^-2 mol L-1}\\ [\ce{HCOOH}] &= \pu{1 * 10^-2 mol L-1}\\ K_{z-\ce{CH3COOH}} &= \pu{1.8 * 10^-5 mol L-1}\\ K_{z-\ce{HCOOH}} &= \pu{1.8 * 10^-4 mol L-1}\\ [\ce{H3O+}]_1 &= \pu{1.3 * 10^-3 mol L-1}\\ [\ce{H3O+}]_2 &= \pu{4.0 * 10^-4 mol L-1} \end{align}

Seeing that we could write $$\ce{HCOOH + CH3COOH + 2H2O -> HCOO- + CH3COO- + 2H3O+},$$ we can derive a equilibrium \begin{align} \frac{[\ce{HCOO-}][\ce{CH3COO-}][\ce{H3O+}]^{2}} {[\ce{HCOOH}][\ce{CH3COOH}]} &= \frac{[\ce{HCOO-}][\ce{H3O+}]}{[\ce{HCOOH}]} \frac{[\ce{CH3COO-}][\ce{H3O+}]}{[\ce{CH3COOH}]}\\ &= K_{z-\ce{HCOOH}}K_{z-\ce{CH3COOH}}. \end{align}

I think we still need to know the original concentrations of $\ce{CH3COOH}$ and $\ce{HCOOH}$, we can calculate $$[\ce{CH3COO-}] = \frac{[\ce{CH3COOH}]}{[\ce{H3O+}]_2} K_{z-\ce{CH3COOH}} = \pu{4.5000 * 10^-4 mol L-1}.$$ For $[\ce{HCOO-}]$ we get $\pu{1.3846 * 10^-3 mol L-1}$ (keeping some significance). \begin{align} n_{\ce{HCOOH}} &= \pu{1.1385 * 10^-2 mol L-1} &&\text{(total)}\\ n_{\ce{CH3COOH}} &= \pu{5.225 * 10^-3 mol L-1} && \text{(total)} \end{align}

Solving for $y$ (neglecting the already present $\ce{H3O+}$ of water) \begin{align} K_{z-\ce{HCOOH}} &= \frac{[\ce{HCOO-}][\ce{H3O+}]}{[\ce{HCOOH}]}\\ &= \frac{x(x+y)}{(0.5n_{\ce{HCOOH}}-x)} \end{align} gives $$y = -0.00018 - x + \frac{1.02465 \cdot 10^{-6}}{x},$$ using $y$ in \begin{align} K_{z-\ce{CH3COOH}} &= \frac{[\ce{CH3COO-}][\ce{H3O+}]}{[\ce{CH3COOH}]}\\ &= \frac{y(x+y)}{(0.5n_{\ce{CH3COOH}}-y)} \end{align} gives $$x = 0.000884322 \vee x = 0.00690291$$ (there are more solutions, but these are the only real positive ones). From this we can calculate $$y = 0.0000943623 \vee y = -0.00693447.$$ $y$ should be positive, thus $x = 0.000884322$ and $y=0.0000943623$. This gives us a $pH$ of $$\mathrm{pH} = -\log(0.000884322+0.0000943623) \approx 3.01$$

Which seems to me as correct (it will be slightly more acidic than when adding the amounts of $\ce{H+}$).

Answer 3

Using concentrations and not activities, user GRSousaJr presents the exact solution to the problem in equations 1-8. However the simplifications don't really seem appropriate. This is a chemistry problem, not a problem in numerical analysis to solve. The gist is that we can make some simplifications based on the number of significant figures and a knowledge of the chemistry.

RANT - I wish book problems would use significant figures consistently. The concentrations are only given to 1 significant figure as are the pH values from which the pKa's can be calculated (rather than looked up). 2 or 3 significant figures would be appropriate, but 4 is definitely too many.

Chemistry - Since both solutions are around pH=3, the final pH must be around 3 too. So $\ce{[H+]} \gg \ce{[OH-]}$ and the charge balance can be expressed as:

$$\ce{[H+] \approx [A-] + [B-]}\tag{6a}$$

that leads to:

$$\ce{[H+] =}\dfrac{C_{\mathrm{HA}}\cdot \mathrm{K_{a,HA}}}{\ce{[H+]} + \mathrm{K_{a,HA}}} + \dfrac{C_{\mathrm{HB}}\cdot \mathrm{K_{a,HB}}}{\ce{[H+]} + \mathrm{K_{a,HB}}}\tag{7a}$$

solving this leads to: \begin{align} \begin{split} &\ce{[H3O+]}^3\\ +&\ce{[H3O+]}^2 (K_{\mathrm{a},(\ce{HA})} + K_{\mathrm{a},(\ce{HB})})\\ +&\ce{[H3O+]}\left( K_{\mathrm{a},(\ce{HA})} K_{\mathrm{a},(\ce{HB})} - (C_\ce{HA} K_{\mathrm{a},(\ce{HA})} + C_\ce{HB} K_{\mathrm{a},(\ce{HB})}) \right)\\ -&\left( (C_\ce{HA} + C_\ce{HB}) K_{\mathrm{a},(\ce{HA})} K_{\mathrm{a},(\ce{HB})} \right)\\ =&\ 0 \end{split}\tag{9a} \end{align}

Since $\ce{[H+]} \approx 10^{-3}$, $\ce{[H+]^3}\approx 10^{-9}$

and $\left( (C_\ce{HA} + C_\ce{HB}) K_{\mathrm{a},(\ce{HA})} K_{\mathrm{a},(\ce{HB})} \right) \approx (0.01)* 2\cdot10^{-4} * 2\cdot 10^{-5} \approx 4\cdot10^{-11} $

Thus the term $\left( (C_\ce{HA} + C_\ce{HB}) K_{\mathrm{a},(\ce{HA})} K_{\mathrm{a},(\ce{HB})} \right)$ is on the edge of what can be neglected.

We know $C_\ce{HA} = C_\ce{HB} = 0.005$, and let's use $K_{\mathrm{a},(\ce{HA})}= 1.778\cdot10^{-4}$ and $K_{\mathrm{a},(\ce{HB})} = 1.754\cdot10^{-5}$ then:

$\ce{[H3O+]}^3 + 1.953\cdot10^{-4} * \ce{[H3O+]}^2 -9.734\cdot 10^{-7‬} * \ce{[H3O+]} - 3.119\cdot10^{-11} = 0 \tag{9b}$

Plugging the equation into Wolfram Alpha yields $\ce{[H3O+]} = 0.000910902 \ce{->[round]} 0.00091 $, $\mathrm{pH} = 3.0405 \ce{->[round]} 3.04 $

For yucks solving:

$\ce{[H3O+]}^2 + 1.953\cdot10^{-4} * \ce{[H3O+]} -9.734\cdot 10^{-7‬} =0 \tag{9c}$

yields $\ce{[H3O+]} = 0.000893781 \ce{->[round]} 0.00089 $, $\mathrm{pH} = 3.0487 \ce{->[round]} 3.05 $

---

Note - I took chemistry in high school and college from 1968-1973. At that time I only ran into a very very few problems that had a cubic and those could be solved by a couple of iterations. In my day I used 4 place logarithms or my slide rule. I didn't get a calculator until grad school about 1975. Not sure if using equation solvers in chemistry classes is allowed now or not.

Answer 4

How would be the equation and the ICE table, and what is the pH of the mixture of these two solutions?

There are three equations:

$$\ce{HCOOH <=> H+ + HCOO-}$$ $$\ce{CH3COOH <=> H+ + CH3COO-}$$ $$\ce{H2O <=> H+ + OH-}$$

Hydroxide is a (very) minor species, so you can neglect it. As I explain below, at the pH of the mixture, the acetate ion is also a minor species, so you can first neglect the dissociation of acetic acid, and then correct for it later.

I would not use an ICE table in this situation, at least not one that describes all three reactions.

My strategy to determine the pH of the mixture

First, you can determine the equilibrium constants for each acid from the pH values of their aqueous solutions (before mixing). The corresponding pKa values are 3.74 and 4.78 for formic and acetic acid, respectively.

After mixing, the concentration of total formic acid and total acetic acid drop by a factor of 2 (mutual dilution). Formic acid is the stronger acid, and would have a pH of 3.06 at this concentration in the absence of acetic acid (less acidic than pH = 2.9 because of dilution).

At pH 3.06, acetic acid dissociates very little (the difference between pH and pKa is more than 1.5, vs. less than 0.7 for formic acid). As a first approximation, we can say that the pH is determined by the stronger acid.

To figure out how much the presence of acetic acid does influence the pH, we can calculate how much it would dissociate at pH 3.06, and correct the pH accordingly. Our new pH will be more acidic, so we assumed a too acidic pH in our correction, overshooting a bit. After a couple of iterations of this, the pH comes out as 3.04.

So the biggest effect of adding the acetic acid comes from diluting the formic acid (pH would go from 2.9 to 3.06 just by adding water). A secondary effect comes from acetic acid dissociating a tiny bit, giving a pH of 3.04.

Here are results from the spreadsheet used for the calculations:

And here are the formulas used (to dampen the overshooting effect, the pH value used in each step is the average of the updated pH and the previous pH, not shown)

I tried to do $\mathrm{pH}=\frac{1}{2}\left(\mathrm{pH}_1+\mathrm{pH}_2\right)$, but it’s trivial and doesn't work.

To convince yourself once and for all that pH averaging does not work, consider these two extreme examples:

1. Mixing 5 mL of 1 M HCl with 6 mL of 1 M NaOH (starting pH values are 0 and 14, resulting pH is roughly 13).

2. Mixing 10 ml of 1 M HCl with 90 mL of water (starting pH values are 0 and 7, resulting pH is 1)

Answer 5

$-\log[\ce{H}]=\text{p(H)}$ you can calculate concentration of $[\ce{H}]$ for each acid, then add the $[\ce{H}]$ for two acids and calculate $\text{p(H)}$ by $-\log[\ce{H}]$.