Let us for simplicity discuss RHF formalism. For $2n$-electron system we have $n$ Hartree-Fock equations written for $n$ spatial orbitals $\{ \phi_{k} \}_{k=1}^{n}$ $$ \newcommand{\mat}[1]{\boldsymbol{\mathbf{#1}}} $$ \begin{equation} \hat{F}(1) \phi_{k}(1) = \varepsilon_{k} \phi_{k}(1) \, , \quad k = 1, 2, \dotsc, n \, . \end{equation} Once we introduce finite basis $\{ \chi_{q} \}_{q=1}^{m}$ and express spatial orbitals as a linear combination of basis functions $\chi_{q}$ \begin{equation} \phi_{k}(1) = \sum\limits_{q=1}^{m} c_{qk} \chi_{q}(1) \, , \quad k = 1, 2, \dotsc, n \, . \end{equation} we end up with $n$ Roothaan–Hall equations \begin{equation} \sum\limits_{q=1}^{m} F_{pq} c_{qk} = \varepsilon_{k} \sum\limits_{q=1}^{m} S_{pq} c_{qk} \, , \quad k = 1, 2, \dotsc, n \, , \end{equation} which can be rewritten in the following matrix form \begin{equation} \mat{F} \mat{c}_{k} = \varepsilon_{k} \mat{S} \mat{c}_{k} \quad k = 1, 2, \dotsc, n \, . \end{equation} The Fock matrix $\mat{F}$ and the overlap matrix $\mat{S}$ are both $m \times m$ square matrices, $\mat{c}_{k}$ is a column $m \times 1$ matrix, $\varepsilon_{k}$ is just a scalar value.

We can then collecl all $n$ $\mat{c}_{k}$ column $m \times 1$ matrices into one $m \times n$ matrix $\mat{C}$ and all $n$ values $\varepsilon_{k}$ into $n \times n$ square matrix $\mat{\varepsilon}$ \begin{equation} \mat{F} \mat{C} = \mat{S} \mat{C} \mat{\varepsilon} \, . \end{equation}
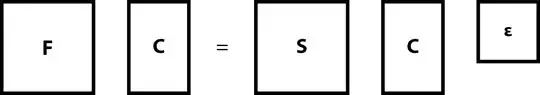
In practice, however, we extend both $\mat{C}$ and $\mat{\varepsilon}$ to $m \times m$ matrices from $m \times n$ and $n \times n$ respectively, which results in having $m-n$ virtual (unoccupied) orbitals.
Taking into account that virtual orbitals are even more unphysical than their occupied counterparts the question is what is the point of such extension of $\mat{C}$ and $\mat{\varepsilon}$? Why do not we just leave them of $m \times n$ and $n \times n$ sizes respectively?