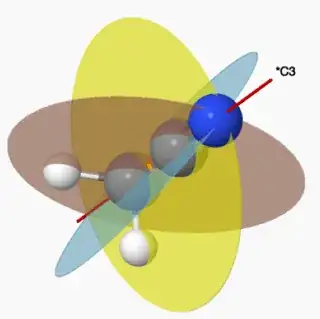
Methyl chloride belongs to the $C_{3\mathrm{v}}$ point group. This is because it has a $C_3$ axis down the $\ce{Cl-C}$ bond.
However what I do not understand is how it has three vertical mirror planes? It has three planes down each of the $\ce{C-H}$ bonds, but don't these bisect a bond making them dihedral planes? Although I'm wrong I can't fathom why it isn't a $C_{3\mathrm{d}}$ point group. I have used a molecular viewer to visualise it but I still get the vertical mirror planes bisecting a bond...