Consider a formazanate ligand. Then imagine an electron-withdrawing group added to it. I expect a small σ-donating effect, and good π-accepting properties.
My supervisor tells me that an electron-withdrawing group causes a lowering of the π*-orbital energy, leading to a smaller $\Delta_\mathrm{T}$ in the d-orbital splitting of the resulting iron-based molecular orbitals. Why would this be the case?
Since not many people know the ligand formazanate (I hadn’t heard of it before this question), let me quickly supply an image of what it looks like:
Scheme 1: General formazane structure.
Coodination happens from the lower two nitrogens, one of which is deprotonated (hence -ate) and both of which chelate the metal with $\mathrm{sp^2}$-type orbitals. The five formazane atoms form a π system, which can be extended by appropriate $\ce{R}$-groups. And one of these $\ce{R}$-groups is now modified to include an electron-withdrawing group.
I already previously gave a qualitative orbital scheme for a tetrahedral complex including σ and π interactions as given below.
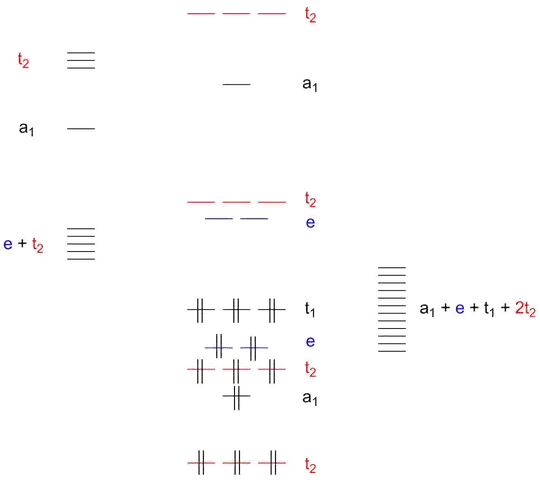
Figure 1: Qualitative MO-scheme of a tetrahedral $\mathrm{d^0}$ complex with σ and π interactions. Originally created for this answer.
The σ donor orbitals transform according to $\mathrm{a_1 + t_2}$, leaving $\mathrm{e + t_1 + t_2}$ for the π ligands. Unfortunately, the picture is a tad clouded, since both σ and π interactions have a $\mathrm{t_2}$ contribution.
Adding an electron-withdrawing group to your ligand will leave the σ interaction unchanged in first approximation, since mainly the ligand’s π system would be affected. The orbital energies of the π system would be reduced. Since we are talking about a metal with a low oxidation state, its orbitals are higher than drawn in the qualitative scheme (which was designed for permanganate). And thus also, the most important π interaction of the ligand will be, as you stated, accepting electrons into its π system.
The exact nature of any effect observed will depend on the original orbital energies. However, the $\mathrm{e}$ orbitals are only affected by the π interaction while the $\mathrm{t_2}$ orbitals are also affected by the σ interaction. The magnitude of π interaction is expected to be the same for both groups of orbitals, since the start from the same value on each side. Thus, the difference between $\mathrm{e}$ and $\mathrm{t_2}$ stems mainly from σ interactions which only affect $\mathrm{t_2}$ due to symmetry.
Because the σ interaction starts with the ligand orbitals being much lower in energy than the metal orbitals, reducing their energy even more will result in a weaker interaction, therefore a lowering of the $\mathrm{t_2}$ level and thus a smaller $\Delta_\mathrm{T}$ or $10~\mathrm{Dq}$ value.
