Your conception of $\pi$-bonds is a bit too restrictive. A $\pi$-bond is a bond in which there is one node along the internuclear axis. So, yes, two side-on $p$-orbitals do form a $\pi$ bond because there is one node along the internuclear axis (the one separating the bottom lobe from the top lobe). A $\sigma$-bond is a bond with no nodes (i.e. cylindrically symmetric), a $\delta$-bond has two nodes, etc. It's important to note that these symmetry labels work best in molecules where each bond axis either exactly lines up with or is exactly orthogonal to all the others (like diatomics and octahedral metal complexes) but we can work in other molecules with a little more effort.
Now, in osmium, the valence orbitals most involved in bonding are actually the $d$-orbitals. Unfortunately, because the molecule has tetrahedral symmetry and the bond axes are not all orthogonal or parallel, it's less easy to see how the oxygen and osmium orbitals come together to form $\pi$ bonds, and we need to resort to MO theory to get a qualitatively correct answer. If you don't know MO theory, the most basic way of approaching the following is to think of all the ligands and metal orbitals combining (much like the simple $p-p$ overlap in your question) and we label each combination by a label that has to do with the symmetries (rotations and reflections) of the combination of atomic orbitals.
Let's start with a qualitative MO diagram from this answer:
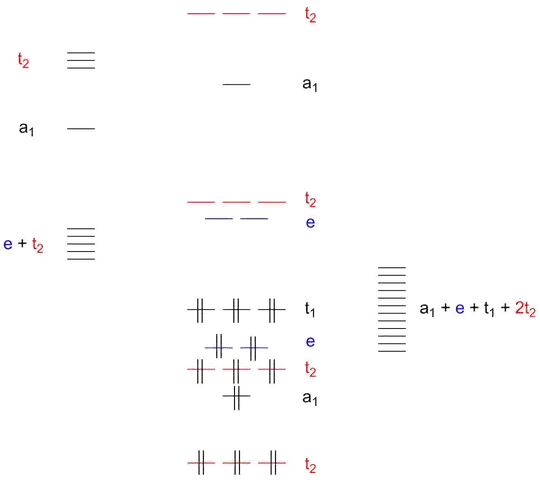Figure 1: Qualitative MO scheme of a tetrahedric complex with σ and π bonding between metal and ligands. Double vertical lines represent electron pairs. Orbital energies here are qualitative (and in fact the order is wrong here for $\ce{OsO4}$ which has occupied orbitals energies $t_1>t_2>a_1>t_2>e$).
The oxygen $p$ orbitals that point toward the metal and will make up the $\sigma$ bonds form the $a+t_2$ orbitals. The oxygen $p$ orbitals that make up the $\pi$ bonds are the $e+t_1+t_2$ orbitals. The osmium $d$ orbitals are $e+t_2$. Since only orbitals of the same symmetry can mix, the $e$ orbitals are purely $\pi$-bonding while the $t_2$ orbitals are a mix of $\pi$ and $\sigma$ bonding.
So your picture is sort of correct for the oxygens but they have to be combined in specific ways in order to overlap with the osmium. Here is a picture of one of the $\pi$ bonds in this molecule:
You can see the $p$ orbitals on each oxygen, the node along the bond axis and the osmium $d$ orbital at the center taking part.
Here is a purely $\sigma$ orbital:
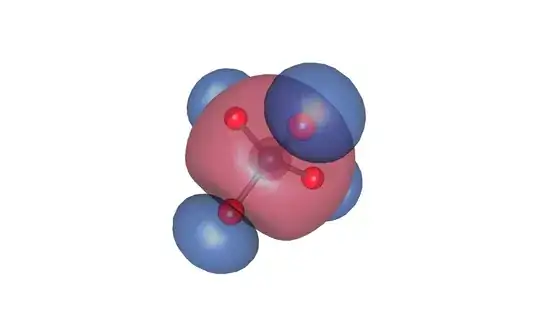
In this case, the Os $s$ orbital participates with the oxygen $p$ orbitals pointing towards the center.
And here are two views of one of those weird $t_2$ orbitals, which is a mix of both $\sigma$ and $\pi$ in tetrahedral symmetry:
You can see that the oxygen $p$ orbitals clearly have a node near the O, but as you get towards the metal center the node bends off-axis. Meanwhile, near the metal, the nodes are not oriented near the bond axes at all. Very confusing!
In tetrahedral symmetry, some orbitals are clearly $\pi$-type, some are clearly $\sigma$-type, and some are a mix and therefore not a well-defined $\sigma$ or $\pi$.
EDIT: The careful reader will note that I ignored the $t_1$ orbitals. These are $p$ orbitals on the the oxygens that have no osmium orbitals to bond with and so are non-bonding. Here is a picture of one of these non bonding orbitals.
You can clearly see all the oxygen $p$ orbitals, but note that the osmium center has no orbital.
