3

I was reading "TFHE Deep Dive" from Ilaria Chillotti, and I am a bit confused over the sample given in 31:08 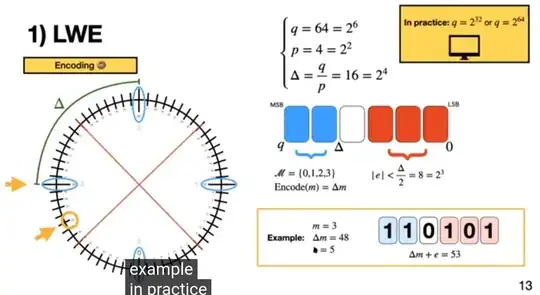enter image description here In the above toy sample, isn't it possible to directly eliminate noise by shifting ciphertext by $\Delta$, then by Gaussian Elimination yielding plaintext?

In general, while intuitively original LWE hardness make sense (errors taken from $D_{L,r}$ with $r\geq \eta_\epsilon(L)$, so support of error cover then whole modulus), I don't really understand how are schemes keeping noise completely separate from plaintext (like above) secure, can't I just discard the noisy bits and do regular gaussian elimination ...?

This is probably a dumb question. Thanks for the reply :)

xade93
  • 51
  • 4

1 Answers1

4

Discarding the noisy bits just means that you are "overwriting" that noise with new noise, essentially.

If $b = as + e$ and the norm of $e$ is bounded by $2^k$, then zeroing the noisy bits means that you are computing $u = b \bmod 2^k$ and $b' = b - u$. Notice that the $k$ lowest bits of $b'$ are zero. But what you obtained is just $b' = as + e - u$. Also notice that since $b$ is random, $u$ is also so (although it is known).

Therefore the noise is always there anyway.

Hilder Vitor Lima Pereira
  • 6,484
  • 21
  • 40
  • What I mean is to perform rescale over the entire ciphertext $(a,b)$, rather than the $b$ term only. A rescale homomorphically performs division and round to nearest element, hence removing the lower bits containing noise, leaving a valid encryption of zero with no noise. Having said that though, I am not really sure how to homomorphically perform division, aside from knowing CKKS being able to achieve it. – xade93 Mar 15 '23 at 05:24
  • Zeroing the lowest bits takes values from $\mathbb{Z}_q$ and outputs values of $\mathbb{Z}_q$ again. Rescaling is different because it also reduces the modulus. That is, if you divide a ciphertext whose noise is $e$ by some $D$ that divides $q$, then you output a ciphertext with noise close to $e/D$ but modulus $q/D$. So the relative noise is essentially the same, i.e., $(e/D) / (q/D) = e / q$, thus the "security of both ciphertexts" is basically the same (remember that the hardness of LWE depends on the ration "norm of noise" over "ciphertext modulus"). – Hilder Vitor Lima Pereira Mar 15 '23 at 09:22
  • But if $|e|<\frac{D}{2}$, does that mean rescale lead to valid encryption with zero noise? since $(e/D)=0$ – xade93 Mar 16 '23 at 11:23
  • e/D is not zero. Round(e/D) would be zero in this case, but you don't round the error when you round the ciphertext. Moreover, there are actually other noise terms included by the rounding. I suggest that you check my answer here to see the exact equations. – Hilder Vitor Lima Pereira Mar 16 '23 at 15:29