Has anyone seen this trick before?
Let's say I'm working with a real pure tone signal that's dangerously close to Nyquist. So, I want to upsample it by a factor of two to move it near the four samples per cycle range. I happen to know the frequency to about 4 or 5 significant digits, so I figured there must be a way to interpolate this without having to do a huge sinc interpolation.
Here's what I came up with. The code explains the math the best (procedurally, but not conceptually or contextually):
import numpy as np#============================================================================= def main():
N = 7 M = 1.234 alpha = 2.95 phi = 2.345 print " Samples per cycle:", 2.0 * np.pi / alpha print "Percent of Nyquist:", 100.0 * alpha / np.pi print whoops = 1.001 factor1 = np.cos( 0.5 * ( alpha * whoops ) ) factor2 = 0.25 / factor1 x = np.zeros( N ) y = np.zeros( 2 * N ) for n in range( N ): x[n] = M * np.cos( alpha * n + phi ) d = 2 for n in range( 1, N-1 ): y[d] = x[n] y[d+1] = x[n] * factor1 + ( x[n+1] - x[n-1] ) * factor2 d += 2 for d in range( 2 * N ): s = M * np.cos( alpha/2.0 * d + phi ) print " %2d %10.6f %10.6f %10.6f" % \ ( d, y[d], s, y[d] - s )#============================================================================= main()
Now, generally my whoops is a lot smaller than the one in the code, but I put it in there to get a feel for the behavior of this approach. Starting in the four samples per cycle range makes the impact of the "whoops" a lot smaller.
Samples per cycle: 2.12989332447 Percent of Nyquist: 93.90141642420 0.000000 -0.862747 0.862747 1 0.000000 -0.960759 0.960759 2 0.678954 0.678954 0.000000 3 1.105637 1.090643 0.014994 4 -0.470315 -0.470315 0.000000 5 -1.197629 -1.180614 -0.017014 6 0.244463 0.244463 0.000000 7 1.245792 1.227380 0.018412 8 -0.009666 -0.009666 0.000000 9 -1.248365 -1.229229 -0.019136 10 -0.225485 -0.225485 0.000000 11 1.205253 1.186094 0.019159 12 0.000000 0.452385 -0.452385 13 0.000000 -1.099553 1.099553
Works well enough for me. I don't think I've ever seen anything like it, but that doesn't necessarily mean a lot.
I've extended the same technique to the triple case, which means 3/2 can be done really cheap too because I have no use for tripling.
Yes, it does look sort of like a Taylor approximation, but it is indeed exact when whoops is one.
Update:
If I am the first to find this trick, I want to claim that and write it up properly. Otherwise, it's move along folks, nothing to see here. This will work at all frequencies up to Nyquist.
Near Nyquist, or for other upscaling factors (U) use:
fudge = ( alpha * whoops )
slice = fudge / U
factor1 = np.cos( slice )
factor2 = np.sin( slice ) / ( 2.0 * np.sin( fudge ) )
Note that the double angle formula for Sines lets me save a $\cos^{-1}$ and $\sin$ calculations, as is done in the code above. I get $\cos(\alpha)$ as a result of my frequency formulas. Which is very convenient.
For the $U=3$ case:
d = 3
for n in range( 1, N-1 ):
stunted = x[n] * factor1
differ = ( x[n+1] - x[n-1] ) * factor2
y[d-1] = stunted - differ
y[d] = x[n]
y[d+1] = stunted + differ
d += 3
You can unroll this loop by a factor of 2 for efficient 3/2 upsampling.
I can't think of a better forum to reach the experts in this field to tell be if this has been done before. Clearly it is not well known or somebody would have answered already.
As per RB-J implicit request, the conceptual math version:
$$ x[n] = M \cos( \alpha n + \phi ) $$
$$ \begin{aligned} x[n+d] &= M \cos( \alpha ( n + d ) + \phi ) \\ &= x[n] \cos( \alpha d ) - M \sin( \alpha n + \phi ) \sin( \alpha d ) \\ \end{aligned} $$
$$ \begin{aligned} x[n-1] &= x[n] \cos( \alpha ) + M \sin( \alpha n + \phi ) \sin( \alpha ) \\ x[n+1] &= x[n] \cos( \alpha ) - M \sin( \alpha n + \phi ) \sin( \alpha ) \\ \end{aligned} $$
$$ \frac{ x[n+1] - x[n-1] }{ 2 \sin( \alpha ) } = -M \sin( \alpha n + \phi ) $$
$$ \begin{aligned} x[n+1/U] &= x[n] \cos\left( \alpha \frac{1}{U} \right) - M \sin( \alpha n + \phi ) \sin\left( \alpha \frac{1}{U} \right) \\ &= x[n] \cos\left( \alpha \frac{1}{U} \right) + \frac{ x[n+1] - x[n-1] }{ 2 \sin( \alpha ) } \sin\left( \alpha \frac{1}{U} \right) \\ &= x[n] \left[ \cos\left( \alpha \frac{1}{U} \right) \right] + ( x[n+1] - x[n-1] ) \left[ \frac{ \sin\left( \alpha \frac{1}{U} \right) }{ 2 \sin( \alpha ) } \right] \\ \end{aligned} $$
$$ \frac{ \sin\left( \alpha \frac{1}{2} \right) }{ 2 \sin( \alpha ) } = \frac{ \sin\left( \alpha \frac{1}{2} \right) }{ 4 \sin( \alpha \frac{1}{2} ) \cos( \alpha \frac{1}{2} ) } = \frac{ 1 }{ 4 \cos( \alpha \frac{1}{2} ) } $$
Quite Easily Done.
I stand by the post title.


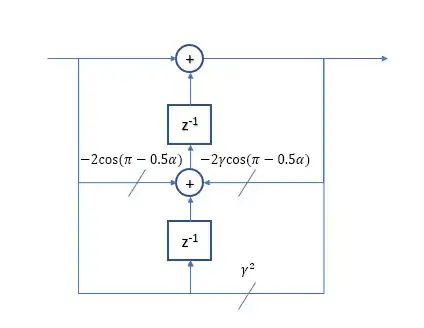

factor, but the higher Fs one gets an extra one depending on its phase difference. It doesn't sound like you want to do tracking, so once the phase difference has stabilised you take that errorfactorand run the faster oscilator from $n=0$ (?) – A_A Jul 22 '20 at 08:34