what is the relationship between these two things
Perhaps more resolution in a spectrogram is equivalent to knowing more the position of the electron and less resolution is knowing the velocity of the electron.
Asked
Active
Viewed 496 times
0
-
2Hi! Um, one is fundamental physical theorem (based on a fundamental math theorem), the other is a method of analyzing a measurement. Neither is about electrons in particular (but Heisenberg's uncertainty principle applies to electrons, too): it's not really clear what you're asking for, specifically. Could you edit your question (don't just comment) to specify why you're asking this, and in which context? Without knowing both, this is too unspecific to be answered. – Marcus Müller Sep 20 '20 at 10:42
-
6Also: You're in the very bad habit of asking a question, getting comments and answers, and not reacting at all to them. That's not how this community works. You might want to go through your question history and at least react to the answers (by either accepting them, if they do answer your question, or commenting on them why they don't). Otherwise,I have little trust in the work someone might put in their answer actually benefitting anyone,and that's detrimental to the overall community as it binds resources through low-effort questions with high-effort answers you don't seem to care about. – Marcus Müller Sep 20 '20 at 10:47
-
Agree with @MarcusMüller here. I was going to explain, but here is link that will require a little studying and a little inference to understand, but I address this connection directly in the "Ideal for a Spectrogram" in https://www.dsprelated.com/showarticle/1365.php. Note that "ideal" here is only along a single evaluative criteria, it is not meant to imply a universal ideal. I do not think your observation is applicable. – Cedron Dawg Sep 20 '20 at 12:52
4 Answers
1
In Quantum Mechanics, state of system specified by a vector (wave function which is a vector in function space), and you could use different basis to represent this vector (imagine one vector in 2 different coordinate system which lead to different components in those coordinate system but they both represent the same vector). For systems composed from moving particles, one basis is the position basis and the second one is momentum basis. The transform between these two basis is the Fourier transform. Considering the wave function give us a probabilistic interpretation, to find the momentum or position of a particle you have to find the average and after that to have a sense about error, you have to find the standard deviation.
The Heisenberg Uncertainty principle, tell us the multiplication of position error and momentum error could not be smaller than some value, for any possible state of system.
Considering this is a property of Fourier transform you could extend that to signals where the signal amplitude and it's spectrum are different representation of same thing in different basis, and say multiplication of effective bandwidth of pulse (as standard deviation of power spectrum around central frequency) and the effective pulse width (as standard deviation of signal's power around it's center in time) could not be smaller than some value for every possible signal.
Mohammad M
- 1,327
- 7
- 13
-
Check out: https://dsp.stackexchange.com/questions/10429/is-the-discrete-gaussian-kernel-an-eigenfunction-of-the-dft – Cedron Dawg Sep 22 '20 at 08:05
-
@CedronDawg I've read your discussions, and i have to say those are far beyond my knowledge. BTW how electrodynamics is related to Fourier transform eigenfunctions? – Mohammad M Sep 22 '20 at 10:22
-
MM, I don't know. I'm sort of getting back into Physics in a hobby style after, yikes, almost 40 years. Closest I've come to someone else exploring the connection is this:
"Anomaly of the Electromagnetic Duality of Maxwell Theory", Hsieh, et al. $$ $$ <5% Comprehension, but a roadmap. The eigenfunction seems to be the discrete Heisenberg narrowest pulse when viewing that level with a discrete paradigm.
– Cedron Dawg Sep 22 '20 at 13:13 -
My conjecture is this: $$ \text{ There is no such thing as a whirlpool, there is only air and water. } $$ $$ \text{ There is no such thing as a particle, there is only vacuum and ether. } $$ I know they will tell me that 'ether' is an outdated concept. They also said exact frequency formulas weren't possible. I had an insight based on refraction, fluid dynamics, and stable flow patterns. – Cedron Dawg Sep 22 '20 at 13:13
-
1@CedronDawg , very nice. I'm not in a position to suggest scientific topics to you, but when I was an undergraduate student one of my favorite courses was statistical mechanics (a very good book on the subject, statistical physics of particles by Mehran Kardar, it may require some background on thermodynamics). Also another topic was calculus of variations (Calculus of variations by Gelfand, also one chapter of Classical Dynamics of Particles and Systems by Thornton). Personally found these topics very interesting and extremely useful, also related to signal processing. – Mohammad M Sep 22 '20 at 14:27
1
Maybe this answers your question:
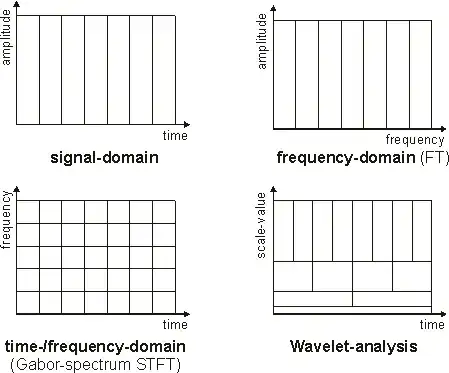
source: (older thread: Which time-frequency coefficients does the Wavelet transform compute?)
Bulbasaur
- 217
- 1
- 10
0
The standard spectrogram (in the complex and redundant form) is a linear transformation that unfolds a 1D time signal onto a 2D time-frequency space. There, each coefficient represent a "time-times-frequency" square whose dimensions correspond to the standard-deviations or second-order moments of the Weyl-Heisenberg inequality for Fourier analysis.
Higher dimensional versions exist.
Laurent Duval
- 31,850
- 3
- 33
- 101
0
The spectogram is a specific member of a class of tools used for time-freq analysis of signals.
The time-freq analysis of a signal may be performed by a number of tools, but most common is to use a time dependent Fourier transform (or a wavelet transform) which is a Fourier transform applied on a sliding window accross the whole signal length.
Such a time-freq analysis provides not only a spectral view of the signal (inside the window) but also its time information of the events in it.
An event is something a like a pulse, a transient, a time-varying frequency of sinusoid (a modulated signal). These signals carry information both in their frequencies and in their timings.
The time-freq analysis has a frequency-resolution determined by the window length & shape, and a time-resolution determined by the window jumps.
A shorter window will provide a better time localisation (resolution) of a particular event, whereas a longer window will provide a better frequency resolution. The dilemma between the short and long windows for better time and frequency resolutions is reminiscent of a well known dilemma from quantum physics which was stated as Heisenberg's uncertainty principle.
Therefore, it's analogously named as the uncertainty principle of signal processing. But there's no physical link in between the two. It says that you cannot increase time and frequency resolutions simultaneously. If one is increasing, then the other must decrease. And their product, which is constant for a given observation time, is called the capacity of analysis.
Unless you increase the total observation interval (per sampling frequency) and thus increase the capacity of analysis, your frequency & time resolutions will be inversely dependent on the other.
Fat32
- 28,152
- 3
- 24
- 50
-
This is the erroneous 'Jacobsen' interpretation of the uncertainty principle. You are simply talking about bin widths with that, nothing more. The Heisenberg/Gabor uncertainty has to do with a pulse width going through the FT. A gaussian is the eigenfunction of the CTFT. Make it wider, and the output is narrower and vice versa. For some parameter it is the same. The analogous (should that be discretous?) situation for the DFT is the eigenvectors found in my latest article. – Cedron Dawg Sep 23 '20 at 12:36
-
@CedronDawg Jacobsen interpretation ??? In signal processing the time-freq localisation uncertainty is about simultaneously resolving the frequency and timing of signals. And that's all about observation window length. Not much interested in your articles. Unfortunately, your lack of experience & literature in the field of (electrical) engineering somehow limits your ability to clearly describe yourself... You are lacking technical clarity. It's hard to distinguish the novel from gimmicks in them. And no one would spend time to do so. It's your duty to use the standard language. – Fat32 Sep 23 '20 at 13:24
-
Tongue in cheek reference to this commonly held misperception. The term "bin width" is standard, sometimes also called "frequency resolution" which is misleading in itself. I have no such duty. Nor does EE "own" this domain. Jacobsen used it explicitly to explain to me quite clearly that an exact frequency formula is "impossible". Horse/water/drink. Ain't my duty to make the horse drink either. It's there if you want to look at it. – Cedron Dawg Sep 23 '20 at 13:31
-
@CedronDawg Unfortunately, it's observed increasingly in the latest decades that due to an excessive competition among collegues, unbreakable prejudice among profs, and a lack of sufficient control on the publishers, several hazardous mechanism have emerged, that can publish trash into web and even into the offical papers. So many papers claim doing so many things but they r either fake (gimmick) or they achieve something that's not verifiable by the claims they propose... Day by day it's getting harder to find true authentic fidelity in the scientific field accross the world. – Fat32 Sep 23 '20 at 13:33
-
That might be true. But you will find fidelity to math in my articles and derivations without reliance on Calculus. And the best frequency formulas in the world, independently tested and verified. To drink, or not to drink, that is the question for you here. http://www.tsdconseil.fr/log/scriptscilab/festim/index-en.html Funny thing, when my work is finally recognized as it should have been long ago, august professors are going to have to cite a dog. :-) – Cedron Dawg Sep 23 '20 at 13:36
-
@CedronDawg I don't care what happened between you and Jocob. Your exact frequency formula equation was correct and I said this to you before. But it's not a big thing in signal processing. Becuase it's rather an algebraic accomplishment to exactly solve a nonlinear equation, but this is not an achievement in signal processing. That's the problem you are not recognising... – Fat32 Sep 23 '20 at 13:36
-
Oh no, I quite recognize that practically it isn't a big improvement over existing techniques, always have. The significance is theoretical, that is what you don't seem to recognize. We have gotten the chat prompt, and I am so tired of bickering. – Cedron Dawg Sep 23 '20 at 13:40
-
@CedronDawg It's neither practically nor theoretically important, but quite nice. as it's not practically applicable and also not someting critical in the theory of signal proocessing. If you really want to achieve something theoretically or practically important in the field, you may deal with finding roots of two dimensional polynomials or you may work on the lacking fundamental theorem of polynomials in 2D that would be helpful in image/video 2D processing techniques. Efficient conversion of nonuniform samples to uniform from polar to cartesian is also of importance. Just work on these. – Fat32 Sep 23 '20 at 13:46
-
-
Thanks for the suggestions, but I have other things I am more interested in. The latter is what my articles are all about, they are way more efficient. The importance of something is a subjective measure, give it time and it can change. I answered the other part of your question in https://dsp.stackexchange.com/questions/70394/dft-coefficients-meaning under Dan's answer in case you missed it. I also added the punchline to the meta post which has subsequently (and mercifully) been closed (Don't remove it). Hope you get a chuckle out of it. You type fast, but I am still done here. Thanks. – Cedron Dawg Sep 23 '20 at 13:54
-
Not quite, I guess. Just a quick point to clarify the above. In PV=nRT, simplified to PV=K. Is there an "uncertainty principle" at work between pressure and volume? Rhetorical question. – Cedron Dawg Sep 23 '20 at 14:00
-
This one isn't worth taking flak over, but you have me really pondering this. Presuming my stuff, or somebody else's, coming from the outside, not adhering to convention, but valuable to the field, was made known. Who's "duty" would/should it be to convert and assimilate it? My experience with professors has been they are more than happy to talk about their findings and work and very reluctant to look at other stuff, especially before it is "officially published". – Cedron Dawg Sep 23 '20 at 23:01
-
When a French guy arrives at the New York airport, which language should he speak to communicate around: French, German, or English? Can he expect everbody to speak his own language, or will he speak their language? If you want to post something into the DSP literature, you should speak the language of the existing community, unless you are an alien invader of course !!! ;-)) – Fat32 Sep 24 '20 at 09:46
-
Or overlord? Cue the Immigrant Song by LedZep. Behave yourselves or the rocks drop. False analogy, another fallacy. You guys should really add debate classes to the EE curriculum, the quality has been low. And where does the astounding arrogance come from? You should drop those classes to make room. (OLGD is EE, you know) Chat prompt and all (PK, thank you for your service), hope you all enjoyed the show. Walks off the stage humming "I'm Sammy the Eighth, I am, I am...." – Cedron Dawg Sep 24 '20 at 11:37
-
@CedronDawg Dont take this place as a representative of EE. That would be a great mistake. You'r right that EE curriculum lacks a critical thinking class. It's already FULL of math-phys-comp. But basic proof methods, necessary & sufficient conditions, contrapositions etc. are missing even in Calculus books! Engineering education is not a place to make philosophical discussions though. Students are taught the fundamental rules and how to apply them. EE has the greatest dept in abstract matters though. But I claim most mathematicians can't write the code that a DSP guy takes for granted. – Fat32 Sep 24 '20 at 12:45
-
@CedronDawg winning a discussion might mean a lot for some sort of people, but it has no place in the discipline of engineering. In ours, it's the applications that are the proofs. Being a good demagogue may bring you some esteem and self satisfaction, but it will seldom help you find a more efficient, accurate, robust, and cost effective solution to a practical problem in life. You must see these points before making such comments here. – Fat32 Sep 24 '20 at 12:48
-
@CedronDawg There are a lot of guys who double in EE and MATH. So If you consider a more serious track in your EE studies, you may at least try an EE masters in DSP field. That would help you a lot to gain what you need. Indeed being good at applied math is a great bonus for EE students in any field of it. – Fat32 Sep 24 '20 at 12:56
-
@CedronDawg If you think that pursuing a masters in EE is too hard for you, then you could still enroll in self-study activities, from the acclaimed books among the curriciulum. Have you studied Signals & Systems and Discrete-Time Signal Proccessing form Opp ? If not, these should be your first books to read and solve all the exercises. Alternative books exist. I can give you a list of necessary books to read and learn to excell in signal processing (or EE in general). – Fat32 Sep 24 '20 at 13:02