As it has proven in some paper and books the time and frequency resolution of Morlet wavelet is :
$\Delta t=\frac{f_c\sqrt{f_b}}{2f_i}$
$\Delta f=\frac{1}{2\pi f_c \sqrt{f_b}}$
I don't know how these relations have obtained, I have asked it in detail in here.you can answer that if you want.
but lets accept these relationship for now. there is some misunderstanding for me in here about the concept of resolution.
for this case, by increasing the term $f_c\sqrt{f_b}$ we have finer frequency resolution but poor time resolution. I am sure about finer frequency and poor time resolution because my practical results meet it. but if you look at $\Delta t$ and $\Delta f$ relationships you receive that increasing the term $f_c\sqrt{f_b}$ leads to decrease $\Delta f$ and increase the $\Delta t$.
does it mean that smaller value of resolution spell to have finer resolution and vice verca?
-
In your last sentence: Smaller value of what resolution? Finer resolution of what? For each resolution, exactly what are you measuring or describing? – hotpaw2 Apr 11 '14 at 22:01
-
I mean does it mean that smaller value of frequency resolution ($\Delta f$)spell to have finer frequency resolution? and moreover does it mean that smaller value of time resolution ($\Delta t$)spell to have finer time resolution? @hotpaw2 – SAH Apr 12 '14 at 04:42
2 Answers
Indeed, that's the Heisenberg Uncertainty Principle - you can't have both very good frequency and time resolution. You always have to sacrifice something. In case of Short Time Fourier Transform it's straightforward, but for wavelets are being 'squeezed', which is changing their frequency resolution. Figure below describes more than a thousand words:
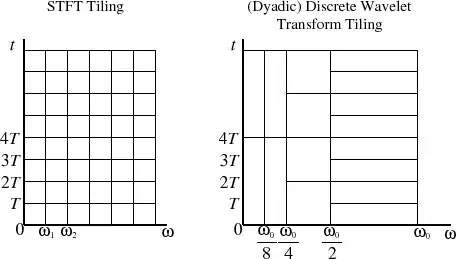
EDIT: Because you are still trying to understand why it is like that, then please mind that by increasing the frequency of the wavelet ($f_c$), you should also shrink it in time (decrease $f_b$). For more info please refer for example to: Paul Addison - The Illustrated Wavelet Transform Handbook. You can find there a following graphs (Section 2.12):



-
Thanks for you info, but I am well aware of that. but this is nothing to do with my question. please check the question again. @jojek – SAH Apr 11 '14 at 21:13
-
1If this has nothing to do with your question, you need to rephrase your question. – MackTuesday Apr 12 '14 at 00:50
-
@MackTuesday The question is fine, I am just asking something about the concept of resolution. $\Delta f$ is said frequency resolution in many paper. and also they said increasing $fc \sqrt{f_b}$ leads to increase(finer) the frequency resolution. but if you look at $\Delta f$ relationship,you will see that $\Delta f$ is proportional to inverse of $fc \sqrt{f_b}$. this happens for $\Delta t$ as well. – SAH Apr 12 '14 at 04:54
-
There's a problem with the diagrams in this answer. The left hand tiling is correct for a linear frequency axis. The right hand diagram for the wavelet tiling should then refer to the same frequency axis, but it doesn't. It is only correct for a log-scale frequency axis, because the time-frequency area of the tiles is constant, the lower and wider tiles would have to be less high, namely by a factor of 2 (for this dyadic lattice) for each row. Therefore I think the diagrams can be quite misleading for a novice. – Jazzmaniac Apr 12 '14 at 08:25
-
@jojek, are you asking whether the diagram you linked in your comment is better? Yes. – Jazzmaniac Apr 12 '14 at 08:57
-
@Jazzmaniac this is not my question.lets just think of frequency now, I want to know why higher resolution ($\Delta f$)causes to have a poor resolution? in the best case scenario the frequency resolution ($\Delta f$) must have a high value or less value in order to distinguish closely spaced frequencies? – SAH Apr 12 '14 at 09:47
-
@Electricman, if this doesn't answer your question then I don't understand your question either. – Jazzmaniac Apr 12 '14 at 13:58
-
well you are all thinking about Heisenberg uncertainty principle and dyadic windows. I am aware of them, but what I am asking is more basic level. I saw in a paper that frequency resolution for Morlet wavelet is define as: $\Delta f=\frac{1}{2\pi f_c \sqrt{f_b}}$ , also practically I know increasing the term $f_c\sqrt{f_b}$ leads to have a finer resolution, but if you look at $\Delta f$ formula you will see that increasing the term $f_c\sqrt{f_b}$ must make $\Delta f$ smaller. so I am confused, smaller value for resolution $\Delta f$ means finer resolution.? @Jazzmaniac – SAH Apr 12 '14 at 14:50
-
@Electricman, a smaller uncertainty means a finer resolution, yes. If your uncertainty is $\Delta f$ then your resolution is proportional to $1/{\Delta f}$. – Jazzmaniac Apr 12 '14 at 16:24
-
thanks loads @Jazzmaniac So, simply what do you suggest me to call $\Delta f$ and $\Delta t$ in my document. I cannot call them frequency and time resolution, because for example, by decreasing $\Delta f$ the frequency resolution is increased. so I want a new name for $\Delta f$ and $\Delta t$. should I call them
frequency and time uncertainty value for Morlet wavelet? or do you have a better idea to name these parameters, calling them as resolution is misleading. coz they are proportional to the inverse value of them. – SAH Apr 12 '14 at 17:00 -
1@Electricman, yes, I think calling them uncertainties or just deviations is fine. You can even call them resolutions, but then make clear that smaller values indicate higher resolution! – Jazzmaniac Apr 12 '14 at 19:27
Increasing the numerical value of delta X usually means the same thing as decreasing the resolution of X, not increasing the resolution of X. However delta X is often called "resolution" in spite if this inverse slope relationship. But you have to be clear in your context about whether you are increasing the numerical value of delta X, or the quality of delta X (its resolution of X), which can have opposite meanings.
- 35,346
- 9
- 47
- 90