Finding where signal is showing some (unknown) periodicity

Question

I have readings of the vertical displacement of someone over time, as in the picture below:

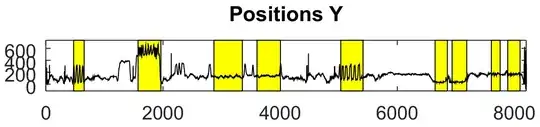At some points in time, the person will be exercising or jumping up & down, creating more or less obvious periodic motions (yellow regions of the graph). I am now trying to find a way to automatically spot these yellow areas, by looking for periodicity in the recorded signal.

My initial attempt has been to use a spectrogram, using the specgram built-in function in Octave: segmentLength=150; window=hanning(150); overlap = 80% * segmentLength; specgram(x, segmentLength, 1, window, overlap)

Which results in the following output:

This seems to be hinting in an ok direction since I see for example that something gets picked up just before frame 2000, however it is not very conclusive. Given my limited understanding of the spectrogram, I am not sure how to proceed from here.

Is the spectrogram the right approach? If yes, how can I improve the output? If no, what approach would you recommend for this task? I am aware that some of the windows that I am trying to identify will be too difficult, but was expecting to at least pick up windows 1, 2 and 5 (starting from the left). Thanks for any pointers!

EDIT

I have tried to implement a simple ASDF in octave with the following code:

#Parameters for asdf analysis
  N=400; %Window size
  kmin= 12;
  kmax= 40;
  step = 50;

  n0min = floor((N+kmax)/2);
  n0max= size(x,2) - floor((N+kmax)/2) -1;
  Q=zeros(kmax-kmin+1, floor((n0max-n0min)/step)+2);

  i=1;
    for k= kmin : kmax %i

    j=1;
    for n0= n0min : step : n0max %j
      for n= 1 : N-1
        Q(i, j) = Q(i,j) + ( (x(n+n0-n0min) - x(n+n0-n0min+k))^2 * hanning(N)(n+1) );
      end
      Q(i, j) = (2/N) * Q(i,j);
      j++;
    end

    fprintf('Calculated %d out of %d periods \n', k-kmin+1, kmax-kmin+1);
    fflush(stdout);

    i++;  
  end

  imagesc(Q)

Tweaking around with the parameters, I ended up with the ones shown in the code, that yield the following result:

This is already getting closer to what I expected. Other suggestions welcome :)

Answer 1

If you're gonna use ASDF to measure periodicity and you want to window the data with something other than rectangular window, do it after subtracting and squaring:

$$ Q_x[k, n_0] \triangleq \frac{2}{N} \sum\limits_{n=0}^{N-1} \left(x[n+n_0-\left\lfloor \tfrac{N+k}{2}\right\rfloor] \ - \ x[n+n_0-\left\lfloor \tfrac{N+k}{2}\right\rfloor + k] \right)^2 w\left(\tfrac{n}{N}\right) $$

where

$\left\lfloor \cdot \right\rfloor$ is the floor() function and, if $k$ is even then $ \left\lfloor \frac{k}{2}\right\rfloor = \left\lfloor \frac{k+1}{2}\right\rfloor = \frac{k}{2} $

and $w\left(\tfrac{n}{N}\right)$ is a window function of non-zero width $N$ samples centered at $n=\tfrac{N}{2}$. A Hann window would be

$$ w(u) \triangleq \begin{cases} \tfrac12 - \tfrac12 \cos(2\pi u) \qquad & 0 \le u < 1 \\ \\ 0 & \text{otherwise} \\ \end{cases}$$

To make this ASDF into "autocorrelation" (in the neighborhood of sample $x[n_0]$) defined from the ASDF:

$$ R_x[k,n_0] = R_x[0,n_0] - \tfrac12 Q_x[k, n_0] $$

where

$$ R_x[0, n_0] \triangleq \frac{2}{N} \sum\limits_{n=0}^{N-1} \Big(x[n+n_0-\left\lfloor \tfrac{N}{2}\right\rfloor]\Big)^2 w\left(\tfrac{n}{N}\right) $$

Since $Q_x[0, n_0] = 0$ and $Q_x[k, n_0] \ge 0$ for all lags $k$, that means that $ R_x[k, n_0] \le R_x[0, n_0] $ for all lags $k$.

Suppose for a minute that $x[n]$ is periodic with period $P$ (and $P$ happens to be an integer), then

$$ x[n+P] = x[n] \quad \forall n $$

and $Q_x[mP, n_0] = 0$ and $R_x[mP, n_0] = R_x[0, n_0] \ge R_x[k, n_0]$ for any integer number of periods ($m$ is an integer). So you get a peak at $k=0$ and at $k$ equal to any other multiple of $P$ if $x[n]$ is periodic. If $x[n]$ is not perfectly periodic, what we might expect is the biggest peak at $k=0$, another peak (but slightly smaller) at $k=P$ (the period we are looking for) and progressively smaller peaks for larger multiples of $P$.

The measure of periodicity in the neighborhood of $n_0$ would be

$$\frac{R_x[P, n_0]}{R_x[0, n_0]}$$

Hmmm, I just thought of something. Because of my audio/music-centric POV, I have been assuming no DC bias (i.e. $x[n]$ should maybe come out of a DC blocking high-pass filter). But I don't think that is the case with your application. So maybe just stick with ASDF, but somewhere you will need a threshold for how low $Q_x[k, n_0]$ can go (for $k \ne 0$) for you to consider that $x[n]$ is periodic in the neighborhood of $n_0$.