I'm honestly lost on creating timing diagrams for bit sequences. I understand for QPSK there are symbols 00, 01, 10, 11 with phase shifts of 45,135,225 and 315.
I'm just not understanding how you get these diagrams. I graphed an example on paper but it doesn't seem consistent (using the bit sequence below).
Maybe I'm a bit lost on the whole even and odd bit sequences.
For example, I'm looking at a bit stream of 01100101 0 (also I assume that lone bit at the end can be written as 00)
So b(t) = 011001010
be(t)=X0100
bo(t)=X1011
E denoting Even, O denoting Odd
Thanks
Edit: Also again, for example, I grabbed this from Wikipedia
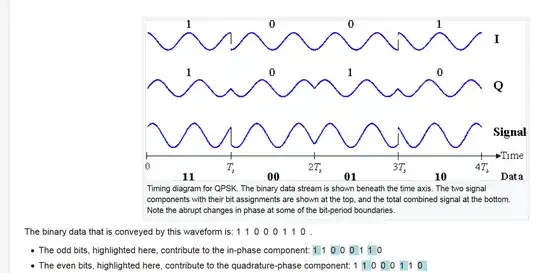
https://en.wikipedia.org/wiki/Phase-shift_keying#Bit_error_rate_2
I feel I'm just missing something that will make it all click. Thanks!
